The “Jump” of Chaitin’s Omega Number
Gregory Chaitin explains, “For any infinity, there’s a bigger infinity, which is the infinity of all subsets of the previous step”In last week’s podcast, “The Chaitin Interview V: Chaitin’s Number,” Walter Bradley Center director Robert J. Marks asked mathematician Gregory Chaitin (best known for Chaitin’s unknowable number) if the unknowable number could prove (or disprove) Goldbach’s Conjecture that every even number can be expressed as the sum of two primes. This task is harder than it first appears because even numbers go on indefinitely. A proof that Christian Goldbach (1690–1764) was right or wrong must show that even numbers must be like that, no matter how big they are or how many of them there are. This time out, Dr. Marks and Dr. Chaitin discuss what we can know about Omega numbers — and where famous mathematicians are buried.
This portion begins at 19:20 min. A partial transcript, Show Notes, and Additional Resources follow.
Robert J. Marks: I’m wondering if there’s any way to get a handle on what Omega prime is.
Gregory Chaitin: Another way to define Omega prime is, it’s not the probability the program will halt, it’s the probability that a program will produce a finite amount of output instead of producing an infinite amount of output. These are programs that never halt, or that may halt, or may not halt. A program that halts obviously only produces a finite amount of output. The property that the program generated at random produces an infinite amount of output…
You talk about programs calculating only one, two, three, four, five. It’s the probability that a program produces all, but a finite number of the positive integers. These are programs that calculate only zero, one, two, three, four, five. The question is, will the numbers that it doesn’t calculate be a finite number of numbers or will it be an infinite number of numbers? That’s Omega double prime.

This was work mostly done by Veronica Becher (pictured) and students of hers, but I participated a little bit in that work. By now it’s probably been generalized and extended in all directions, like happens in pure mathematics all the time.
Robert J. Marks: Well, that’s the thing. Omega itself is mind-blowing. But the fact that there’s a regress into Omega prime and Omega double prime is hyper mind-blowing if you will. And it goes on and on, doesn’t it?
Gregory Chaitin: Yeah. Well this happens also. This hierarchy of things that are more and more unknowable, there’s the normal computer. There’s a computer that has an oracle for the halting problem. Then there’s a computer that has an oracle for the computer that has an Oracle for the halting problem. It goes up and up. It’s a sort of a hierarchy like Cantor’s theory of infinities. There’s infinity of the integers, infinity of the reals. For any infinity, there’s a bigger infinity, which is the infinity of all subsets of the previous step. You have a hierarchy and dare I say that this is the notion maybe that you can only approach God in the limit. I think Georg Cantor [1845–1918] was interested in this question.
Note: “Although many people contributed to the study of infinity over the centuries it was Georg Cantor in the nineteenth century who established its modern development. Cantor created modern set theory and established the importance of one-to-one correspondence between sets. For example he showed that the set of all integers can be put into one-to-one correspondence with the set of all fractions and so these two sets have the same infinity. But he also proved the remarkable result that there are infinitely many infinities, all of different sizes.” – Raymond Flood, Gresham College
Robert J. Marks: In fact, I believe that Cantor attempted to gain an audience with Pope Leo the XIII about his theory of transfinite numbers. He never got to the Pope, but he got to one of his subordinates because he thought about the theological implications of his theory.
Gregory Chaitin: Absolutely. I regard Cantor’s theory of infinities as a mathematical theology. It’s beautiful stuff. It’s also paradoxical. Apparently Cantor thought that God was speaking to him. He felt he was inspired. In a way, anyone who is creative sounds like God is speaking to us. In mathematics that I would say is discovered not invented, you feel you’re touching a reality beyond normal reality.
This is in that 90-minute BBC Four documentary, Dangerous Knowledge:
It’s in five parts and I give the links on my website with the original poster that BBC Four used. I think it’s a wonderful movie. The gentleman who made it, David Malone, actually went out to the places where all this work was done.
Also, in some cases, to the cemeteries where these amazing mathematicians, or philosophers or theologians, or physicist in case of Boltzmann, are buried. Maybe it’s not obvious that when he talks about one of these thinkers, he’s actually showing you where he worked and maybe where he’s buried and things like that. It’s like a mathematical travel documentary. It’s quite a fun film.
Robert J. Marks: I’ve always found that interesting. We know what these people do, but not who they were. I think visiting the grave sites kind of tells us who they were.
Gregory Chaitin: I visited Gödel’s and von Neumann’s grave sites at Princeton.
Robert J. Marks: You did? Oh they’re buried in Princeton, I didn’t know that.
Gregory Chaitin: Buried in the cemetery. That’s a short walk from the Princeton University.
Robert J. Marks: I see. Is Einstein buried there also, do you know?
Gregory Chaitin: No. Einstein insisted that he be cremated and the ashes be scattered at an undisclosed location.
He didn’t want to leave a shrine. I also visited Gödel’s home, which is near the cemetery. It’s in a poor part of town. Von Neumann had a home that I never visited unfortunately. I only found out where it was, it’s in the wealthy part of Princeton. They’re together in the same cemetery, rather close to each other.
Anyway, I visited Gödel’s home and the people who are renting it from the current owner let me in. They showed me things that were left there from when Gödel was the inhabitant. For example, he had soundproofing put in because noise distracted him enormously.
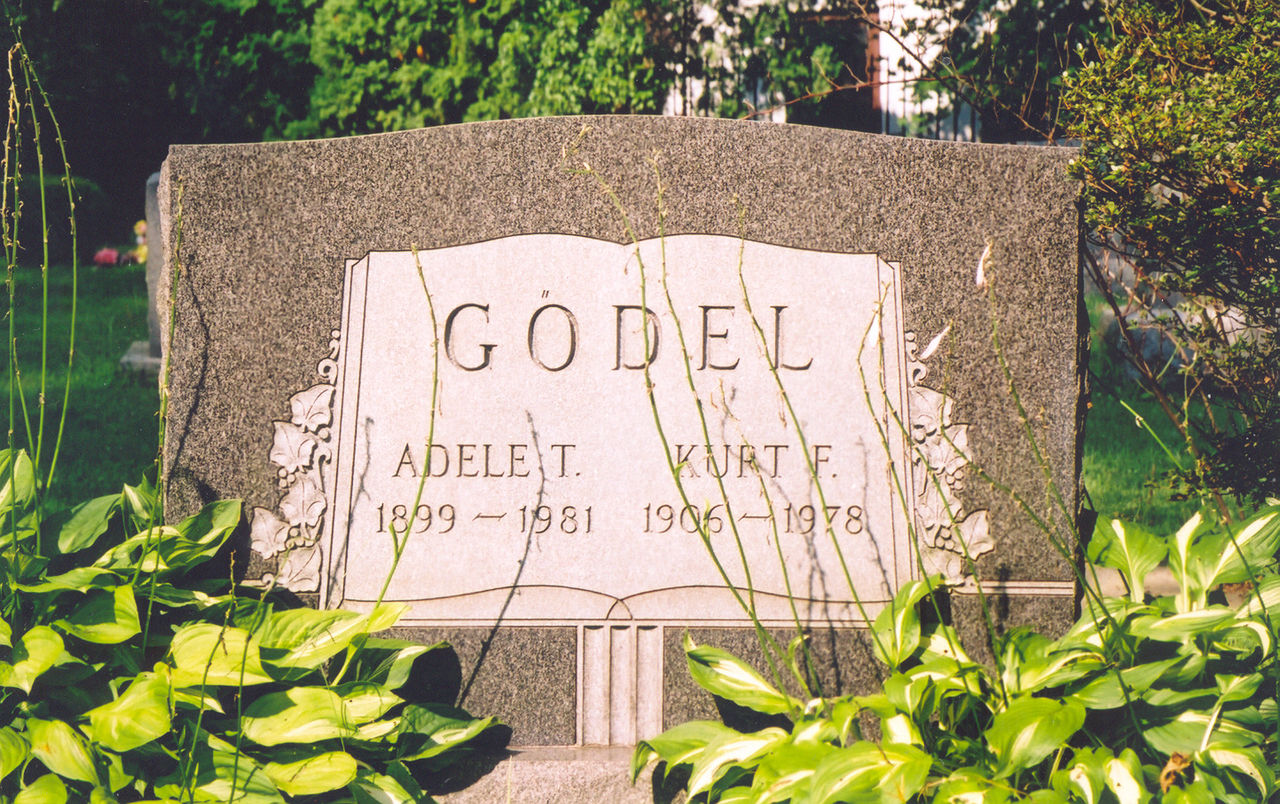
His wife had a shrine to the Virgin Mary in the backyard, which was still there. In fact, their home was in the neighborhood which, when they bought the home, was for Italian laborers, people who did construction work, I think.
It was in a relatively modest part of town. Gödel didn’t marry a professor’s daughter. He married a woman he fell in love with, from comparatively humble origins. I think she felt more comfortable [there]. Also, it was a Catholic neighborhood, whereas Princeton, of course, was some form of high Protestantism I believe, at that time.
Note: Here. is a “mathematical tour of the Princeton Cemetery,” featuring the graves of many persons of mathematical interest.
Don’t miss the stories and links from the previous podcasts:
From Podcast 5:
Could Chaitin’s Number prove Goldbach’s Conjecture at last? Chaitin notes that the problem grows exponentially and the calculations get quite horrendous. Gregory Chaitin acknowledges that the Omega number doesn’t solve all problems but the Omega prime or Omega double prime might help.
Why “impractical” things like philosophy are actually quite useful. Chaitin argues that the human spirit is capable of doing both practical things and impractical things which may have practical consequences later. Gregory Chaitin reflects on the fact that if he had to do practical work 60 years ago, there wouldn’t be practical research today based on the Omega number.
Chaitin’s number talks to Turing’s halting problem. Why is Chaitin’s number considered unknowable even though the first few bits have been computed? Chaitin explains, after you have computed some of the numbers, all the rest looks totally random and unstructured and you’ll never know them.
Is Chaitin’s unknowable number a constant? One mathematics team has succeeded in the first 64 bits of a Chaitin Omega number. Gregory Chaitin explains that it’s more complicated than that; it depends on whether you use a universal Turing machine that allows for very concise programs.
From Podcast 4:
Can mathematics help us understand consciousness? Gregory Chaitin asks, what if the universe is information, not matter? Some philosophers see the universe as created by mathematics, not matter. Gregory Chaitin prefers to see it as created by information. God is then a programmer.

Why human creativity is not computable. There is a paradox involved with computers and human creativity, something like Gödel’s Incompleteness Theorems or the Smallest Uninteresting Number. Creativity is what we don’t know. Once it is reduced to a formula a computer can use, it is not creative any more, by definition.
The paradox of the first uninteresting number. Robert J. Marks sometimes uses the paradox of the smallest “uninteresting” number to illustrate proof by contradiction — that is, by creating paradoxes. Gregory Chaitin: You can sort of go step by step from the paradox of the smallest “uninteresting” number to a proof very similar to mine.
Why the unknowable number exists but is uncomputable. Sensing that a computer program is “elegant” requires discernment. Proving mathematically that it is elegant is, Chaitin shows, impossible. Gregory Chaitin walks readers through his proof of unknowability, which is based on the Law of Non-Contradiction.
Getting to know the unknowable number (more or less). Only an infinite mind could calculate each bit. Gregory Chaitin’s unknowable number, the “halting probability omega,” shows why, in general, we can’t prove that programs are “elegant.”
From Podcast 3:
A question every scientist dreads: Has science passed the peak? Gregory Chaitin worries about the growth of bureaucracy in science: You have to learn from your failures. If you don’t fail, it means you’re not innovating enough. Robert J. Marks and Gregory Chaitin discuss the reasons high tech companies are leaving Silicon Valley for Texas and elsewhere.
Gregory Chaitin on how bureaucracy chokes science today. He complains, They’re managing to make it impossible for anybody to do any real research. You have to say in advance what you’re going to accomplish. You have to have milestones, reports. In Chaitin’s view, a key problem is that the current system cannot afford failure — but the risk of some failures is often the price of later success.
How Stephen Wolfram revolutionized math computing. Wolfram has not made computers creative but he certainly took a lot of the drudgery out of the profession. Gregory Chaitin also discusses the amazing ideas early mathematicians developed without the software-based methods we are so lucky to have today.
Why Elon Musk, and others like him, can’t afford to follow rules. Mathematician Gregory Chaitin explains why Elon Musk is, perhaps unexpectedly, his hero. Very creative people like Musk often have quirks and strange ideas (Gödel and Cantor, for example) which do not prevent them from making major advances.
Why don’t we see many great books on math any more? Decades ago, Gregory Chaitin reminds us, mathematicians were not forced by the rules of the academic establishment to keep producing papers, so they could write key books. Chaitin himself succeeded with significant work (see Chaitin’s Unknowable Number) by working in time spared from IBM research rather than the academic rat race.
Mathematics: Did we invent it or did we merely discover it? What does it say about our universe if the deeper mathematics has always been there for us to find, if we can? Gregory Chaitin, best known for Chaitin’s Unknowable Number, discusses the way deep math is discovered whereas trivial math is merely invented.
From the transcripts of the second podcast: Hard math can be entertaining — with the right musical score! Gregory Chaitin discusses with Robert J. Marks the fun side of solving hard math problems, some of which come with million-dollar prizes. The musical Fermat’s Last Tango features the ghost of mathematician Pierre de Fermat pestering the math nerd who solved his unfinished Last Conjecture.
Chaitin’s discovery of a way of describing true randomness. He found that concepts f rom computer programming worked well because, if the data is not random, the program should be smaller than the data. So, Chaitin on randomness: The simplest theory is best; if no theory is simpler than the data you are trying to explain, then the data is random.
How did Ray Solomonoff kickstart algorithmic information theory? He started off the long pursuit of the shortest effective string of information that describes an object. Gregory Chaitin reminisces on his interactions with Ray Solomonoff and Marvin Minsky, fellow founders of Algorithmic Information Theory.
Gregory Chaitin’s “almost” meeting with Kurt Gödel. This hard-to-find anecdote gives some sense of the encouraging but eccentric math genius. Chaitin recalls, based on this and other episodes, “There was a surreal quality to Gödel and to communicating with Gödel.”

Gregory Chaitin on the great mathematicians, East and West: Himself a “game-changer” in mathematics, Chaitin muses on what made the great thinkers stand out. Chaitin discusses the almost supernatural awareness some mathematicians have had of the foundations of our shared reality in the mathematics of the universe.
and
How Kurt Gödel destroyed a popular form of atheism. We don’t hear much about logical positivism now but it was very fashionable in the early twentieth century. Gödel’s incompleteness theorems showed that we cannot devise a complete set of axioms that accounts for all of reality — bad news for positivist atheism.
You may also wish to read: Things exist that are unknowable: A tutorial on Chaitin’s number (Robert J. Marks)
and
Five surprising facts about famous scientists we bet you never knew: How about juggling, riding a unicycle, and playing bongo? Or catching criminals or cracking safes? Or believing devoutly in God… (Robert J. Marks)
Show Notes
- 00:27 | Introducing Gregory Chaitin and Chaitin’s number
- 01:32 | Chaitin’s number or Chaitin’s constant?
- 07:16 | Must the halting problem be solved for smaller programs in order to get Chaitin’s number?
- 09:50 | The usefulness of philosophy and the impractical
- 17:17 | Could Chaitin’s number be calculated to a precision which would allow for a proof or disproof of something like Goldbach’s Conjecture?
- 19:20 | The Jump of the Omega Number
Additional Resources
- Gregory Chaitin’s Website
- Unravelling Complexity: The Life and Work of Gregory Chaitin, edited by Shyam Wuppuluri and Francisco Antonio Doria
- Elements of Information Theory by Thomas Cover and Joy Thomas
- “On the length of programs for computing finite binary sequences,” by Gregory Chaitin, published when he as a teenager. (Journal of the ACM (JACM) 13, no. 4 (1966): 547-569).
- Chris Calude, professor at the University of Auckland
- Gottfried Wilhelm Leibniz, German Enlightenment philosopher, mathematician, and political adviser
- Stephen Wolfram, computer scientist and physicist
- Goldbach Conjecture
- Collatz Conjecture
- Legendre’s Conjecture
- Elon Musk, engineer and entrepreneur
- G.H. Hardy, English mathematician
- Ray Solomonoff, one of the founders of algorithmic information theory
- Hector Zenil, computational natural scientist
- Automacoin
- Bitcoin
- Marvin Minsky, cognitive and computer scientist
- George Gilder, economist and co-founder of the Discovery Institute
- Twin Prime Conjecture
- Georg Cantor, mathematician
- BBC 4’s Dangerous Knowledge
