Gregory Chaitin on the Great Mathematicians, East and West
Himself a “game-changer” in mathematics, Chaitin muses on what made the great thinkers stand outIn this week’s podcast, “The Chaitin interview I: Chaitin chats with Kurt Gödel,” Walter Bradley Center director Robert J. Marks interviewed mathematician and computer scientist Gregory Chaitin on the almost supernatural awareness that the great mathematicians had of the foundations of reality in the mathematics of our universe:
This discussion begins at 8:26 min. A partial transcript, Show Notes and Additional Resources follow.

Robert J. Marks: There are few people who can be credited without any controversy with the founding of a game changing field of mathematics. We are really fortunate today to talk to Gregory Chaitin (pictured) who has that distinction. Professor Chaitin is a co-founder of the Field of Algorithmic Information Theory that explores the properties of computer programs. Professor Chaitin is also the recipient of a handful of honorary doctorates and a medallion for his landmark work.
Note: To get some sense of Chaitin’s work, see “Things exist that are unknowable: A tutorial on Chaitin’s number” (Robert J. Marks): “Chaitin’s number is an intellectually stunning piece of mathematics, ranking with Cantor’s model of the infinite and Shannon’s theory of information in terms of mind-bending brilliance.
“The number exists. If you write programs in C++, Python, or Matlab, your computer language has a Chaitin number. It’s a feature of your computer programming language. But we can prove that even though Chaitin’s number exists, we can also prove it is unknowable.
“The mathematically provable idea that something exists but is unknowable has clear philosophical and theological implications.”
Robert J. Marks: I know in your work that you looked at things like relativity, this was in your teens for Pete’s sake, and quantum mechanics. And so what led that led you down the path of computer science and to do the founding of Algorithmic Information Theory?
Gregory Chaitin: I was always very interested in computers. They were just starting at the Columbia Science Honors Program. They had a course where the kids could get access to computers. So I started programming in an assembly language. I think also in Fortran. There was a course given by a nice professor and they let the kids run programs on big mainframes, which is what we had then.
I was reading Scientific American. I remember vividly an article on Gödel ’s Proof with a fantastic photograph of Gödel where he angrily leaned at the camera with a blackboard behind him.
Note: Gödel’s Proof: “Kurt Gödel’s incompleteness theorem demonstrates that mathematics contains true statements that cannot be proved. His proof achieves this by constructing paradoxical mathematical statements. To see how the proof works, begin by considering the liar’s paradox: ‘This statement is false.’ This statement is true if and only if it is false, and therefore it is neither true nor false.
“Now let’s consider ‘This statement is unprovable.’ If it is provable, then we are proving a falsehood, which is extremely unpleasant and is generally assumed to be impossible. The only alternative left is that this statement is unprovable. Therefore, it is in fact both true and unprovable. Our system of reasoning is incomplete, because some truths are unprovable.” – What is Gödel’s proof? (Scientific American, February 19, 2006)
Gregory Chaitin: And then in 1958, a book called Godel’s Proof by Ernest Nagel and James R. Newman came out. I was 11. I had permission to take out books from the adult section in the New York City Public Library. I had piles of books at home and I was reading, reading, reading, physics, mathematics. It was a nice time to be a kid growing up in Manhattan.
The discussion turned to 18th-century Swiss mathematician Leonhard Euler (1707–1783), a pioneer in geometry, trigonometry and calculus, among many other fields:

Robert J. Marks: I guess, especially if you’re interested in that sort of stuff. You said you had your hands on some of the original works of Euler (pictured). Do you consider him — I consider him maybe — if not the greatest, certainly the most prolific mathematician in history.
Gregory Chaitin: Yeah, they may still be publishing his collected works. When I was a kid, they were many, many volumes and they were going to be more. He’s my favorite mathematician. As far as I’m concerned, he’s the… It’s sort of silly to rank people. People talk of Gauss as the, I don’t know what they say, the prince of mathematics or something. As far as I’m concerned, it’s Euler. If Gauss is the prince, then Euler is the king.
His papers are beautiful to read. He gives his whole train of thought and it looks obvious. It looks obvious only while you’re reading Euler. Gauss gives very concise papers that are very hard to decipher, but while you’re reading Euler, you think, oh, I could have done this, but of course only Euler could have done this.
Note: Famous quotations from Euler:
● “Mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the human mind will never penetrate.” – Quoted in G Simmons Calculus Gems (New York 1992).
● “Although to penetrate into the intimate mysteries of nature and thence to learn the true causes of phenomena is not allowed to us, nevertheless it can happen that a certain fictive hypothesis may suffice for explaining many phenomena.” – Today in Science History
● “For since the fabric of the universe is most perfect and the work of a most wise creator, nothing at all takes place in the universe in which some rule of the maximum or minimum does not appear.” – Methodus Inveniendi Uneas Curvas (1744), 1st addition, art. 1.
Robert J. Marks: I understand when he lost the sight in both of his eyes, he would sit around in St. Petersburg with students and dictate his ideas to them because he wasn’t able to see.
Gregory Chaitin: But his productivity didn’t go down.
Robert J. Marks: His productivity didn’t go down. Just an astonishing mind.
Gregory Chaitin: Yeah. It’s astonishing because you ask, where did all this creativity come from…? New mathematics, beautiful new mathematics was just pouring out of his head onto the paper and the publishers couldn’t keep up. So his paper…
He had a pile of papers and every now and then somebody would take some of them off the top, I think. And he would keep adding more so they weren’t published in order in which they were done. And when I was reading the collected works of Euler, the Russians had this pile of manuscripts that hadn’t all been included in his collected works yet. And they were being cagey. They were going slow.
Note: Not to neglect German mathematician Carl Friedrich Gauss (1777–1855), “In Gauss’s annus mirabilis of 1796, at just 19 years of age, he constructed a hitherto unknown regular seventeen-sided figure using only a ruler and compass, a major advance in this field since the time of Greek mathematics, formulated his prime number theorem on the distribution of prime numbers among the integers, and proved that every positive integer is representable as a sum of at most three triangular numbers.
“At the age of just 22, he proved what is now known as the Fundamental Theorem of Algebra (although it was not really about algebra). The theorem states that every non-constant single-variable polynomial over the complex numbers has at least one root (although his initial proof was not rigorous, he improved on it later in life). What it also showed was that the field of complex numbers is algebraically “closed” (unlike real numbers, where the solution to a polynomial with real co-efficients can yield a solution in the complex number field).
“Then, in 1801, at 24 years of age, he published his book “Disquisitiones Arithmeticae”, which is regarded today as one of the most influential mathematics books ever written, and which laid the foundations for modern number theory.” – The Story of Mathematics
Feats such as these earned him the moniker Chaitin notes, “Prince of Mathematicians”
Gregory Chaitin: I also had the collected works of Niels Henrik Abel (1802–1829) in my hands, a child prodigy who did some beautiful work. But Euler works on every possible topic. And so where does all this new mathematics, where does this creativity come from? It seems to be, have a supernatural source, as if…
Robert J. Marks: In fact, that’s a topic I want to talk to you about later, whether or not maybe the creativity might be, for example, non-algorithmic, non-computable.
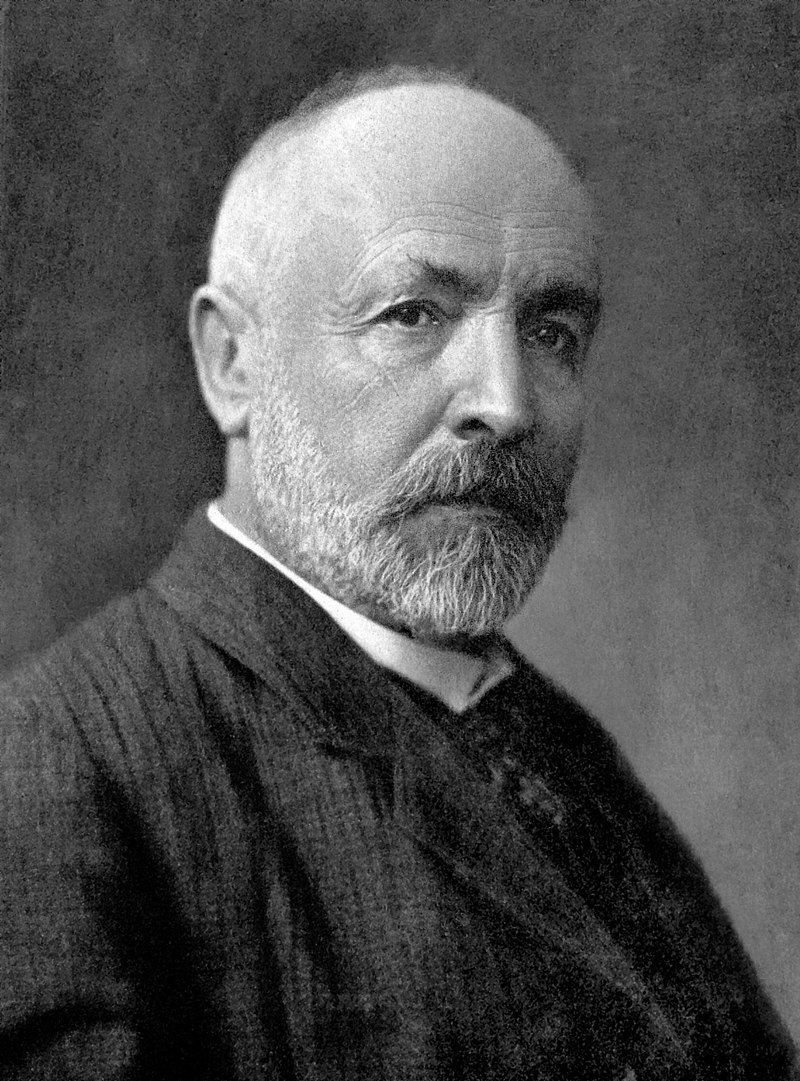
Gregory Chaitin: Maybe God was talking to him. Georg Cantor thought that. Because it’s really hard explain where all those new ideas came from.
Note: Georg Cantor (1845–1918, pictured) is best remembered for being “ perhaps the first mathematician to really understand the meaning of infinity and to give it mathematical precision… Cantor coined the new word “transfinite” in an attempt to distinguish these various levels of infinite numbers from an absolute infinity, which the religious Cantor effectively equated with God (he saw no contradiction between his mathematics and the traditional concept of God).” – The Story of Mathematics
“Cantor also believed that his theory of transfinite numbers ran counter to both materialism and determinism — and was shocked when he realized that he was the only faculty member at Halle who did not hold to deterministic philosophical beliefs.” Liquisearch
Gregory Chaitin: Ramanujan is another example like that. He didn’t have a formal education in math. And he said that there was a Hindu goddess that would tell him mathematics while he slept.

That’s the most reasonable explanation I can think of for how he did that or how Euler did that, unless we work out a complete artificial intelligence and it can do what Cantor or Ramanujan did. For now, I think the best explanation is the one that Ramanujan gave.
Robert J. Marks: Which was a supernatural sort of intervention…
Note: Srinivasa Ramanujan (1887–1920), “The Man Who Knew Infinity,” (pictured) died young of tuberculosis but he had a lasting impact on modern mathematics:
Bruce C. Berndt, Professor of Mathematics at the University of Illinois at Urbana-Champaign: “the theory of modular forms is where Ramanujan’s ideas have been most influential. In the last year of his life, Ramanujan devoted much of his failing energy to a new kind of function called mock theta functions. Although after many years we can prove the claims that Ramanujan made, we are far from understanding how Ramanujan thought about them, and much work needs to be done. They also have many applications. For example, they have applications to the theory of black holes in physics…
“Ramanujan died of his illness on April 26, 1920, at the age of 32. Even on his deathbed, he had been consumed by math, writing down a group of theorems that he said had come to him in a dream. These and many of his earlier theorems are so complex that the full scope of Ramanujan’s legacy has yet to be completely revealed and his work remains the focus of much mathematical research. His collected papers were published by Cambridge University Press in 1927.” – Biography.com
A film of Ramanujan’s life debuted in 2014 and aired at the Toronto Film Festival in 2015:
Next: Gregory Chaitin’s “almost” meeting with Kurt Gödel. This hard-to-find anecdote gives some sense of the encouraging but eccentric math genius
and
How Kurt Gödel destroyed a popular form of atheism We don’t hear much about logical positivism now but it was very fashionable in the early twentieth century. Gödel’s incompleteness theorems showed that we cannot devise a complete set of axioms that accounts for all of reality — bad news for positivism.
You may also wish to read: Things exist that are unknowable: A tutorial on Chaitin’s number (Robert J. Marks)
Note: Chaitin is also the author of Conversations with a Mathematician: Math, Art, Science and the Limits of Reason Springer (October 17, 2001) A free preview is available.
Show Notes
- 00:23 | Introducing Gregory Chaitin
- 05:00 | Chaitin’s Youth
- 06:33 | Chaitin’s journey to computer science
- 08:26 | Chaitin’s thoughts on Leonard Euler
- 12:42 | Chaitin’s near brush with Kurt Gödel
- 17:16 | The quirks of Gödel
Additional Resources
- Gregory Chaitin’s Website
- Unravelling Complexity: The Life and Work of Gregory Chaitin, edited by Shyam Wuppuluri and Francisco Antonio Doria
- Conversations with a Mathematician: Math, Art, Science and the Limits of Reason by Gregory J. Chaitin
- Meta Math!: The Quest for Omega by Gregory Chaitin
- Thinking About Gödel and Turing: Essays on Complexity by Gregory J. Chaitin
- Proving Darwin: Making Biology Mathematical by Gregory Chaitin
- “On the Length of Programs for Computing Finite Binary Sequences” by Gregory J. Chaitin, written and published when he was a teenager
- Leonard Euler, Swiss mathematician and physicist
- Kurt Gödel, Austrian-born mathematician
- Georg Cantor, German mathematician
- Dr. Robert J. Marks’ critiques of Gregory Chaitin’s ideas on Youtube
- “Active Information in Metabiology“: Winston Ewert’s, William Dembski’s, and Robert J. Marks’ paper on Chaitin’s metabiology
You may also wish to read: Five surprising facts about famous scientists we bet you never knew: How about juggling, riding a unicycle, and playing bongo? Or catching criminals or cracking safes? Or believing devoutly in God… (Robert J. Marks)
