Yes, You Can Manipulate Infinity—in Math
The hyperreals are bigger (and smaller) than your average number — and better!Most of us learned the basic number systems in high school—integers (positive and negative whole numbers), fractions (ratios of numbers), real numbers (all those infinitely-continuing decimals), and maybe even complex numbers (with the evil letter “i” lurking around and causing trouble). For most everyday math, these numbers work really well.
However, some types of numbers are not well represented by the real numbers. The real numbers don’t handle numbers that are infinitely large or their inverses—numbers that are infinitely small. At most, the real numbers are extended with the positive infinity (∞ or + ∞) or negative infinity (- ∞) symbols to denote numbers too large or too small for the system to handle. However, the rules of the real numbers prevent any actual manipulation of these symbols. For instance, the relationship ∞ – ∞ is not zero, but undefined.
The hyperreal number system extends the reals so as to handle infinity precisely. Note that there are actually multiple ways to handle infinitely large numbers. But I have found one particular system to be of more practical use than other systems, which is why I think it is worth discussing. Thinking about infinities is somewhat mind-bending, but it turns out that actually manipulating infinities with the hyperreal system is incredibly easy if you are familiar with basic algebra.
For the hyperreals, a new number is introduced to represent infinity. Because the hyperreals are new, there is no universal standard for what the notation for infinity should be, so I usually adopt a lowercase Greek omega (ω). So what is ω, exactly? You should think of ω as a kind of unit but, instead of representing a physical quantity (like a foot or a mile or a kilogram), it represents a numerical quantity that is an infinity.
As we will see, there are many different infinities. So, if we can’t count to infinity (who has the time?) and there are multiple infinities, which particular one is ω? As it turns out, the particular infinity it refers to doesn’t really matter, provided that we are consistent about it. That is, we can say that ω represents some particular infinity. We don’t have to know which one, we just have to agree that it won’t change.
If you need a specific number to imagine, think of a 1 with an infinite number of zeroes following it. Once you have an infinite unit like ω, you can do a lot with it. We can multiply infinity by two and have 2 ω. We can add one to it and have ω + 1. These are all hyperreal numbers. We can even square the infinity and have ω2. What on earth is ω2? Think of it this way: If I have the number 100 (two zeroes at the end) and I multiply it by 100 (two zeroes at the end), I will get the number 10,000 (four zeroes at the end). So, if I take the number ω and multiply it by ω, I will get ω2, which you can think of as having two infinite sets of zeroes at the end.
So, like ordinary mathematical symbols, hyperreal numbers can be added, subtracted, multiplied, and divided. ω + ω is 2ω. ω x ω is ω2. ω7/ω3 is ω4. You can basically treat ω as if it were x, with the exception that it has a few special properties because it is infinite.
Real numbers are basically numbers which have no ω component. Alternatively, you can think about them as being multiplied by ω0 (since anything raised to the zero power is 1).
What if we divide by ω? What is 1/ω or ω-1? This is known as an infinitesimal, an infinitely small value. Because infinitesimals are used so often, it is useful to have a special symbol to refer to them, the lowercase Greek epsilon (ε). If I have, say, 5 + ε, I am referring to a number that is infinitely close to 5. That is, there is no real number that is between 5 and 5 + ε.
Just as we pictured ω as a 1 with an infinite number of zeroes after it, you can picture ε as a decimal looking like 0.0000001, except that there is an infinite number of zeroes between the decimal place and the 1. Likewise, if you have ε2, you can think of it as a number that has two infinite sets of zeroes between the decimal place and the 1.
So, for example, 5 + ε + 7 ε2 is a hyperreal number that is infinitely close to 5 but is slightly further out on the number line than 5 + ε (but not by much!).
How does this help us do math and solve problems? It turns out that the hyperreal number system greatly simplifies several aspects of mathematics. As a simple example, let’s say we have the following equation:
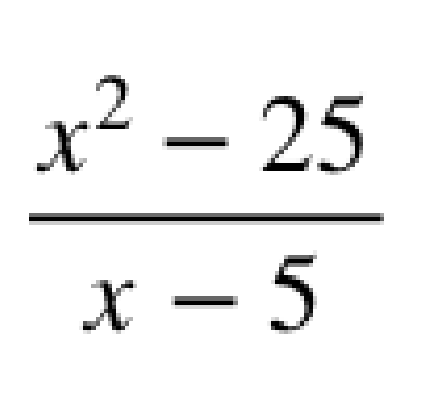
Let’s say that we wanted to find out what the value of this equation was at x = 5. What would we get? We would wind up with:
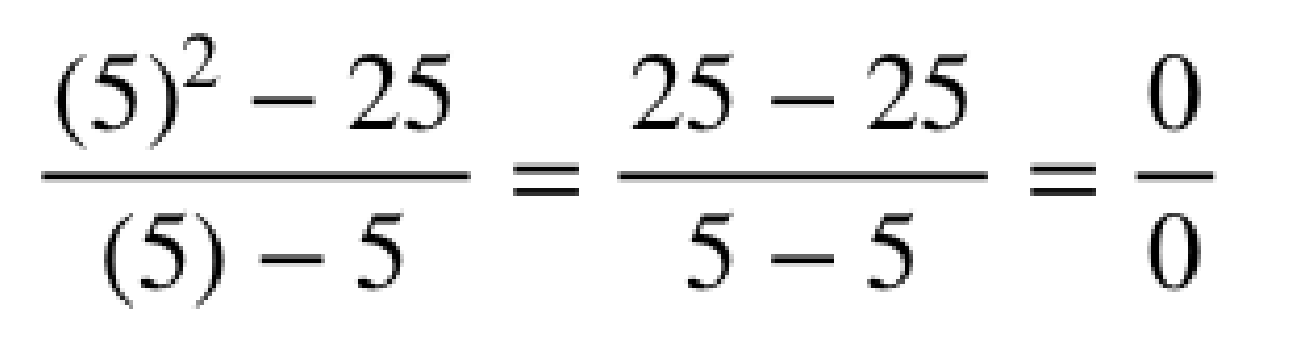
Zero divided by zero is an unknown value. So, if we can’t figure out what this is at x = 5, what if we bumped x just a little bit? What if we looked at x = 5.01? It turns out that this expression only has a problem at exactly x = 5; any other number works perfectly fine. However, with the real numbers, we would have to modify x a small, finite amount to get an answer. However, that will be inexact because we could always choose a value a little closer to 5. For instance, we could have looked at 5.0001 or 5.0000001. But, with hyperreals, we can bump x by an infinitely small amount instead. If we calculate the value at 5 + ε, the calculation will work out to:
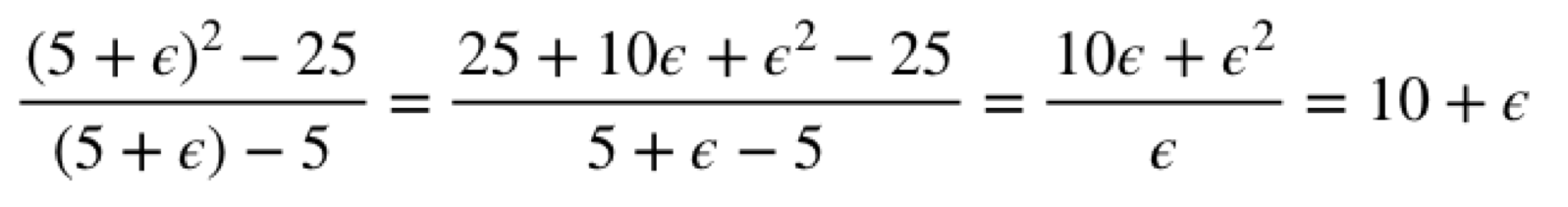
So, the result of this is 10 + ε, which is infinitely close to the number 10. To be explicit, you can use the “standard part” function std to “round” the value to the nearest real number. In other words, std(10 + ε) = 10. Therefore, for the given fraction, we can say, for all practical purposes, when x = 5, the result is 10. This is not impossible to do with real numbers. The concept of a “limit” in the real numbers is very similar to this process. However, limits rely on a lot of proofs and additional rules that are essentially unnecessary when you use hyperreal numbers. With hyperreal numbers, you can simply calculate the values directly.
In short, hyperreal numbers are a new type of number that was developed to simplify and rethink the way that we deal with very large and very small numbers. It reduces the complexity of the task and allows us to use our well-honed high-school algebra skills to solve complex problems easily.
If you enjoyed this discussion of hyperreal numbers, you may also enjoy:
Don’t leave home without these three curves: Three mathematical curves explain a lot of what happens—and doesn’t happen—in everyday life. (Jonathan Bartlett)
and
Things exist that are unknowable. A tutorial on Chaitin’s number (Robert J. Marks)
Here’s Robert J. Marks‘s short five-part series on the unique, reality-defying nature of mathematical infinities:
Part 1: Why infinity does not exist in reality. A few examples will show the absurd results that come from assuming that infinity exists in the world around us as it does in math. In a series of five posts, I explain the difference between what infinity means — and doesn’t mean — as a concept.
Part 2. Infinity illustrates that the universe has a beginning. The logical consequences of a literally infinite past are absurd, as a simple illustration will show. The absurdities that an infinite past time would create, while not a definitive mathematical proof, are solid evidence that our universe had a beginning.

Part 3. In infinity, lines and squares have an equal number of points Robert J. Marks: We can demonstrate this fact with simple diagram. This counterintuitive result, driven by Cantor’s theory of infinities is strange. Nevertheless, it is a valid property of the infinite.
Part 4. How almost any numbers can encode the Library of Congress. Robert J. Marks: That’s a weird, counterintuitive — but quite real — consequence of the concept of infinity in math. Math: Almost every number between zero and one, randomly chosen by coin flipping, will at some point contain the binary encoding of the Library of Congress.
and
Part 5: Some infinities are bigger than others but there’s no biggest one Georg Cantor came up with an ingenious proof that infinities can differ in size even though both remain infinite. In this short five-part series, we show that infinity is a beautiful — and provable — theory in math that can’t exist in reality without ludicrous consequences.
You may also wish to read: Yes, you can manipulate infinity in math. The hyperreals are bigger (and smaller) than your average number — and better! (Jonathan Bartlett)
