Are Divergent Series Really an “Invention of the Devil”?
The real villain in the piece is horrendously non-specific concepts of infinity. But that can be fixedMathematician Niels Abel (1802–1829) is famously quoted as saying, “Divergent series are the invention of the devil, and it is shameful to base on them any demonstration whatsoever.” This general sentiment remains today. So, what are divergent series, and why are they viewed with the suspicion that Abel suggests? And is there a way to use them honestly?
In mathematics, a “series” is a set of numbers that are added together, usually given some formula for the next value. For instance, “1 + 2 + 3” is a series (where the next value is simply the whole number after the previous number), as is “1 + 1/2 + 1/4” (where the next value is half the previous number). An infinite series is just a series where you keep on adding terms forever. Instead of just “1 + 2 + 3”, you have “1 + 2 + 3 + …”. Instead of “1 + 1/2 + 1/4”, you have “1 + 1/2 + 1/4 + …”. In these cases, the … represents the fact that these series have an infinite number of terms.
Another way to write these is with summation notation. Instead of “1 + 2 + 3 + …” we would write:
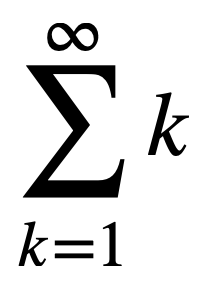
This figure says that the variable “k” will get each number from 1 to infinity, and we are going to add them all up together. The giant, angular symbol is the Greek letter “sigma”, which is used in mathematics to say that we need to “sum” together all of the different values that the formula on the right can represent.
As another example, our sum “1 + 1/2 + 1/4 + …” can be written as:
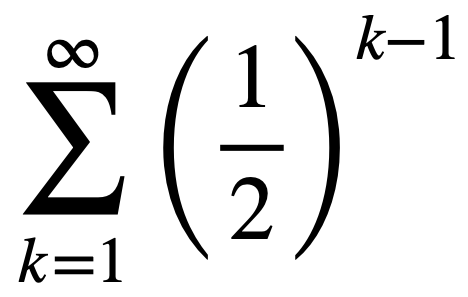
As you may recall from algebra, anything raised to the power of zero is 1. So, with k = 1, the first term will be 1/2 raised to the zero power, which will be one. The second term will be 1/2 raised to the first power, which is just itself (1/2). The third term will be 1/2 raised to the second power, which is 1/4, etc.
So, what is a divergent series?
In the second example (1 + 1/2 + 1/4 + …), note that the numbers we are adding together are getting smaller. In fact, they are getting smaller sufficiently quickly that there is a number that they will get infinitely close to, but never reach. That value is 2. That means that the series converges to the value 2. It will never actually reach it, but it will always get closer to 2, and will get really, really close (i.e., infinitely close).
In the first series we looked at (1 + 2 + 3 + …), the value is getting larger and larger as it grows. There is no limit to how big the series gets. This means that the series is divergent.
Divergent series have been used to prove all sorts of weird things. For instance, some people claim that the sum (1 + 2 + 3 + …), instead of going to infinity, goes to the value -1/12. The proof for this was originally given by the mathematician Srinivasa Ramanujan (1887–1920) and it is proofs like this that led Abel to say what he did about divergent series being an invention of the devil. More formally, Bernhard Riemann (1826–1866) developed the Riemann Rearrangement Theorem, which showed that divergent series can be rearranged to yield any value.
However, as has been recently shown, the real problem with divergent series has been in the treatment of the concept of infinity. It turns out that there are several different conceptions of infinity, and different ones give you different capabilities.
The traditional infinity, ∞, is horrendously non-specific. Depending on how it is used, it essentially means “boundless” or even “outside of the real numbers.” But it is not really more specific than that. At the end of the 19th century, Georg Cantor (1845–1918) introduced two additional concepts of infinity—ordinal and cardinal infinities. While neither of them obeys typical algebraic rules, they are both much more rigorously conceived than the traditional infinity. In the 1960s, a new extension to the number system was developed, the hyperreal numbers. In the hyperreal numbers, infinities obey the traditional algebraic rules. It was the fact that infinities did not obey algebraic rules that led to such strange results with infinite series.
It turns out that using hyperreal numbers (i.e., infinities that obey algebraic rules) resolves many of the paradoxes that previously plagued conceptions of divergent series. It is now possible to assign specific values to divergent series. For instance, the series (1 + 2 + 3 + …) is equal to ω2/2+ ω/2, where ω is the hyperreal version of infinity. For reasons that we won’t go into here, this can be further simplified for all practical purposes to ω2/2. The series (1 + 3 + 5 + …) (i.e., the odd numbers) is equal to just ω2. Therefore, using this system, we can legitimately talk about dividing these two series, and find out that (1 + 2 + 3 + …) / (1 + 3 + 5 + …) is 1/2 (the infinities cancel just like any other multiplier).
For those interested in more, a recent article in Communications of the Blyth Institute by myself and others builds on this topic, showing how many different types of series which required a variety of different analytical tools to analyze and manipulate can be folded in to a single, coherent system using hyperreal numbers. Also see this article here at Mind Matters News on the hyperreal number system.
If you enjoyed this piece, have a look at some of Jonathan Bartlett’s other articles on mathematics:
Yes, you can manipulate infinity in math. The hyperreals are bigger (and smaller) than your average number — and better!
Don’t leave home without these three curves: Three mathematical curves explain a lot of what happens—and doesn’t happen—in everyday life.
Walter Bradley Center Fellow discovers a longstanding flaw in an aspect of elementary calculus. The flaw doesn’t lead directly to wrong answers but it does create confusion.
Often, in life as in calculus, when our implicit assumptions as to why something can’t be done are made explicit, they can be disproven. Calculus textbooks are the most dry and boring presentations of mathematics I have ever seen, even though calculus offers some of the most amazing insights. Unfortunately, most mathematics texts teach only the mathematics, never the insights.
and
Mathematics gives us life skills and mental tools. Unfortunately, some professors, like the one who attacked my recent article, seem to prefer pedantry
Also: Things exist that are unknowable. A tutorial on Chaitin’s number (Robert J. Marks)
