We Need a Better Test for True AI Intelligence
Better than Turing or Lovelace. The difficulty is that intelligence, like randomness, is mathematically undefinableDespite a huge amount of work in the field of artificial intelligence, in philosophy of mind and in neuroscience, there is no consensus as yet on the definition of the “intelligence” part of the phrase.
The most famous attempt at a definition is Alan Turing’s test for intelligence. Turing held that if an artificial process is intelligent, then a human agent engaging in free dialogue with the process cannot differentiate the experience from interacting with another human being.
The Turing test is a subjective definition. It sounds reasonable but if we examine it carefully, we can spot a problem. The condition Turing describes is necessary but not sufficient. That is, evidence of intelligence is a necessary property of intelligence but does not entail it. For one thing, the reverse is not true. The fact that a human being cannot differentiate interaction with a non-human intelligent process from interaction with another human does not entail that the non-human process is intelligent.
Another, more recent, definition of intelligence is the Lovelace test. The test would rate a process as intelligent if an examiner who exhaustively understood its inner workings considered the process’s output to be unexpected.
Again, this appears to be a necessary but not sufficient characteristic of intelligence. For example, if we are flipping a fair coin, we cannot predict ahead of time the outcome of the flips. But there does not seem to be anything mysterious about the mechanics of flipping, nor does the outcome seem intelligent.
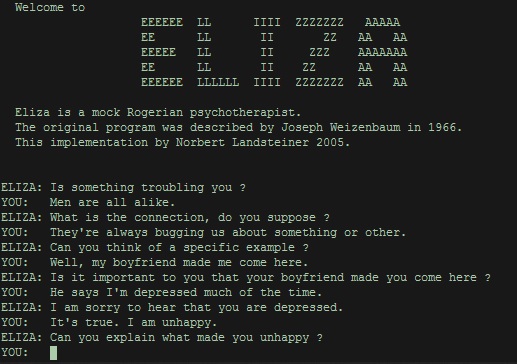
However, the tests are not useless. Even though they cannot define what intelligence is, they can define what intelligence is not. They can eliminate processes that are not intelligent. For example, we could create a set of rules for interacting with a person, such as the famous Eliza program. If we frame things well, the program may seem intelligent for a while. But then we will begin to notice patterns in the way the program responds and we can formulate questions that show that the program cannot really be intelligent. Thus, the Turing test eliminates Eliza from being intelligent.
We can perform a similar analysis with the Lovelace test. After a careful inspection of Eliza’s source code, a programmer can easily predict how Eliza will respond in a given situation. Thus, the Lovelace test also eliminates Eliza as an intelligent process.
These two tests provide a baseline from which we can evaluate a proposed new test. Any process that can pass the new test must also be able to pass both the Turing and the Lovelace tests.
This situation is very similar to the problem faced by mathematicians who are trying to define randomness. There are many tests of randomness, but none of the tests can tell us whether a process is random. The tests can only tell us when a process is not random. It turns out that randomness itself is mathematically undefinable. Kolmogorov proved that we cannot determine if an outcome is random because the algorithmic information of a process is not computable. In a similar way, intelligence itself is mathematically undefinable. However, as with the tests for randomness, we can formulate tests for intelligence that can identify when a process is not intelligent.
Because neither randomness nor intelligence can be mathematically defined, a question arises: Are they the same thing? If it were impossible to differentiate randomness from intelligence mathematically, it would be appropriate to say that, for all intents and purposes, randomness and intelligence are identical.
However, it is possible to mathematically distinguish randomness and intelligence. Such a statement sounds at first like a contradiction in terms; we have just established that neither concepts can be mathematically defined. But the fact that we cannot predict an outcome does not entail we cannot distinguish between outcomes.
As a simple example, imagine that we have two boxes with screens. One box displays random noise on the screen and the other box prints cogent responses when we talk to it. We have no understanding of the inner workings of the boxes or how they generate the images on the screens, nor can we predict what the boxes will display. But we can infer that the two boxes have different modes of operation based on observing the outcomes. This is how we distinguish between randomness and intelligence. The outcomes of the two sources of output look different.
Now let us return to the topic of tests for intelligence. One of the hallmarks of intelligence is the ability to use language. Animals use rudimentary signals, but only human intelligence exhibits a complex grammar that refers to and structures both physical and metaphysical concepts. We use an extensive symbol system to describe events when they are abstracted away from the events themselves. In Tolkien’s Silmarillion, the elves call themselves the Quendi because they discover no other living creature on earth that can speak or sing.
In linguistics, a language hierarchy is recognized; languages can range from simple to complex. At the simplest level are “context free” languages. Their terms can be understood in isolation from the surrounding context. At the most complex level are languages that are “contextual”. These languages require a holistic understanding of the surrounding context, such as we find in human languages.
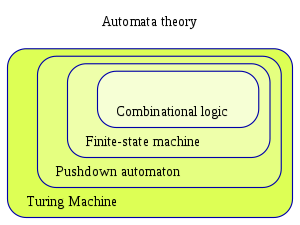
A corollary to the language hierarchy in linguistics is the automata hierarchy in computer science. This is a hierarchy of ever more powerful machines. At the lowest level are “state machines” which are a set of states and kinds of events that transition from one state to the next. Then there are “pushdown automata” which have a memory store. At the highest level are “Turing machines” which are complex enough to copy any other Turing machine, as well as all the machines that are lower down on the hierarchy. Our computers are Turing machines. (A technical point: Turing machines must have unbounded memory, but our computers have limited memory due to our finite universe. However, this is not a problem for the purposes of our analysis.)
An important feature of the automata hierarchy is that each level can recognize more complex kinds of languages. The lowest level can recognize only context-free languages. But contextual languages require memory and thus require pushdown automata or Turing machines. The general principle is that greater complexity in language requires greater complexity in a recognition mechanism.
This correspondence between the linguistic and automata hierarchies suggests another type of intelligence test. For example, we can use language recognition to distinguish between the different levels of automata. If an automaton can recognize a contextual language, then we can tell that it is an automaton with memory. If the language is complex enough, we can infer that the automaton is a Turing machine.
The benefit of this kind of intelligence test, in contrast to the Turing and Lovelace test, is that it is a positive test for intelligence. Notice that with Turing and Lovelace, if an entity passes the test, we cannot say that the entity is indeed intelligent. With the Turing test, there is always the possibility that the human interrogator has not asked the right questions or the program has been framed in such a way as to fool interrogators. At best, we can say that if a program cannot pass the Turing test then the program is not intelligent. Similarly, with the Lovelace test, we saw that flipping a coin would pass the Lovelace test, yet the coin flip is certainly not intelligent. On the other hand, if a program cannot pass the Lovelace test, then the program cannot be intelligent.
Now contrast this with the language test we are considering. We can determine that a language is contextual and we can identify whether a process is able to recognize the language. Thus, we can positively identify a process as at or above a certain position on the automata hierarchy. If we update the language hierarchy to include Turing’s oracle machines at the top, above standard Turing machines and identify the oracle machines with human and greater intelligence, then it is possible to positively test for human and greater intelligence. The key component is identifying a language that is beyond the languages that a Turing machine can recognize.
Is there such a language and, if so, is there anything that can recognize the language? Human language is well known to be very difficult to process with computer algorithms. It is heavily researched in the field of natural language processing. We can see that easily with the Microsoft Word grammar checker and other online grammar recognition tools. These tools are helpful and can find some simple mistakes but they cannot handle even modestly complex grammar recognition. Additionally, a number of basic tasks in natural language processing are known to be inherently computationally complex, meaning that the task becomes exponentially difficult for a computer if the task size increases even slightly. And the general task of language recognition is known to be in the class of problems that are unsolvable for computers because it requires solving the halting problem.
One distinction we need to make is between language recognition and language understanding. For example, a proofreader can spot grammatical errors, structuring problems, and so on in a highly technical and obscure manuscript without understanding the content of the manuscript. This is called language recognition. The proofreader can identify when the manuscript is and is not following the rules and guidelines of correctly formatted writing.
Where does this leave us in our search for a means of testing for intelligence? Let us return to the automata hierarchy with state machines, pushdown automata, and Turing machines. We discussed placing something known as an oracle machine at the top of the hierarchy, above Turing machines. One key feature of the automata hierarchy is that everything above can copy everything below but the reverse is not the case. So, oracle machines can copy everything else on the hierarchy, including Turing machines, but nothing below the oracle machines can copy them. Another important feature of the oracle machine is that the oracular part cannot be a machine. All physical machines can be copied by a Turing machine. But because oracle machines are above Turing machines, they cannot be copied by Turing machines. Because all physical machines can be copied by Turing machines, then oracle-machines cannot be physical machines. And the only significant addition that an oracle machine features is the oracle. Therefore, the oracle is something that lies beyond physical mechanism, i.e., it is non-physical.
So what have we established? We’ve identified that human language is, with very high confidence, unrecognizable for Turing machines. And we’ve established that to recognize more complex languages, we must go higher up on the automata hierarchy. Thus, we must conclude that to recognize human language, we must go higher up the automata hierarchy than Turing machines. Therefore, we need something that is at least as powerful as an oracle machine to recognize human language. Oracle machines are necessarily non-physical, so whatever can recognize human language is also beyond the physical universe.
As a result, with our language test, we can establish whether something is intelligent at the same level as a human being. But we have also seen that anything that can be as intelligent as a human being cannot be implemented with a Turing machine, computer program, or any sort of physical mechanism (including quantum computers). Because the field of artificial intelligence only deals with ways to copy human intelligence with physical machines, then this means that the goal of copying human intelligence with artificial intelligence is impossible.
To round out the analysis with one last sanity check, let us revisit the original intelligence tests: Turing and Lovelace. We mentioned before that if we are going to propose a new kind of intelligence test, then whatever can pass the new intelligence test should also be able to pass the Turing and Lovelace test. In regards to the Turing test, a process that passes the human language test should be able to pass the Turing test. While the process may not be able to converse on every topic of interest to the human, the process will at least be able to recognize the structure of the human’s dialogue and respond in a structurally coherent way.
The more interesting case is the Lovelace test. The Lovelace test requires that the process be unpredictable, even assuming a complete understanding of its operation. Due to the fact that the process must at least be an oracle machine, which is necessarily not a physical mechanism, then it is impossible to understand the process’s operation as a predictable physical mechanism. Thus, the process passes the Lovelace test as well. Incidentally, we also see here that the process that passes the language test is both unpredictable and non-random.
Well, that was quite a lengthy discussion of intelligence testing! But we discovered a better intelligence test and came to a definite conclusion about the nature of human intelligence. We saw that the traditional intelligence tests are flawed because they are only negative tests. On our quest to discover a positive test, we covered the language and automata hierarchies and found out that human language tops both hierarchies. We also arrived at the remarkable conclusion that this means the operation of human intelligence must be non-physical because it transcends Turing machines, which in turn transcend every physical mechanism.
Also by Eric Holloway: Will artificial intelligence design artificial superintelligence?
Artificial intelligence is impossible
and
Human intelligence as a Halting Oracle
