Can an 18th Century Statistician Help Us Think More Clearly?
Distinguishing between types of probability can help us worry less and do more
Thomas Bayes (1702–1761) (pictured), a statistician and clergyman, developed a theory of decision-making which was only discussed after his death and only became important in the 20th century. It is now a significant topic in philosophy, in the form of Bayesian epistemology. Understanding Bayes’ Rule may be essential to making good decisions.
Let’s say that you are a generally healthy person and have no symptoms of any illness and no specific risk factors for any illness. Acting on a friend’s suggestion, you get screened for a variety of diseases, just to be sure. Of the diseases you test for, the HIV test comes back positive. You read on the package that the test is 99.6% accurate. Are you more likely to have the disease or not?
This question might seem simple, but in fact it is not. It is based on a fairly basic misunderstanding of probability. When a test is said to be 99.6% accurate, the test is likely to produce the right data 99.6% of the time. Normally, these numbers are broken out into a “true positive rate” (sensitivity) and a “true negative rate” (specificity) but we have used a single accuracy value for simplifying matters.
Although knowing the accuracy rating of a test is important, when you take a test, you really want to know the answer to a very different question: What is the probability that a positive result means that I have the disease? Although the questions “Is the test accurate?” and “Do I have the disease?” sound similar, they are potentially quite different, as we shall see.
Here’s an explanation: There is a difference between the probability of data given a hypothesis and the probability of a hypothesis given the data. That is, the probability of “getting a positive test” because “I have HIV” is different from the probability of “I have HIV” because “I got a positive test.” They aren’t the same quantities.
Thomas Bayes discovered a way to relate the two quantities to each other. Doing this, however, requires one other piece of information. In this case, the information we need is the incidence of the disease in the population — which, for HIV, is 0.133%.
Bayes realized that the probability of two things occurring at the same time could be calculated in two different ways. The probability that “I have HIV” and “I got a positive test” are both true can be expressed as the probability of “I have HIV” multiplied by the probability of a positive test (i.e., the test accuracy rate).
However, you can also calculate the chances in a different way. You can take the probability that you will get a positive test (for any reason) and then multiply it by the probability that you in fact have HIV if you do get a positive test (this is the probability we actually want to know).
Here it is, in equations. If equations are not your best skill, skip to the explanation below the equations. Otherwise…
Because these two values are equal (they are both equal to the probability of both statements being true simultaneously), they can be set equal to each other and you can solve for the quantity you want. In our case, it looks like this (where “Pr” means “Probability of”):
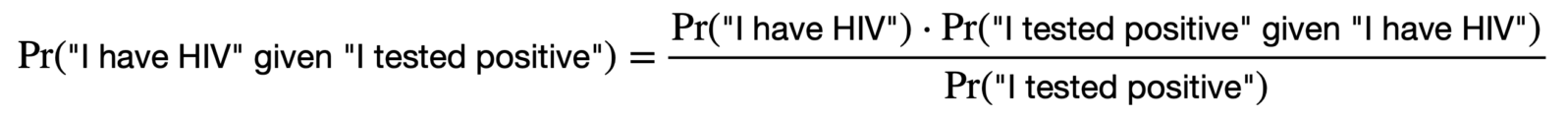
Calculating the total probability of “I tested positive” is a different matter. But, with the incidence of HIV itself very low, we can approximate it to the failure rate (i.e, the opposite of the accuracy rate): 0.4%. So, that gives us:
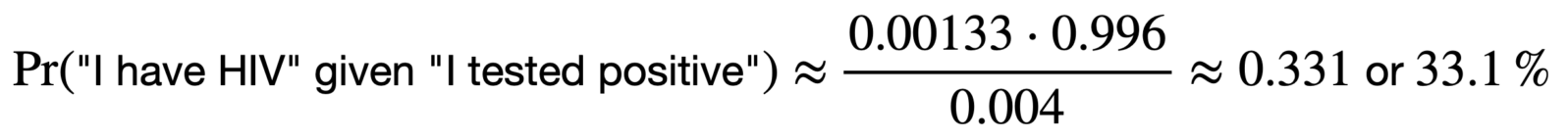
This means that, if you have no reason to believe that you have HIV but a screening test with 99.6% accuracy tells you that you have it, then your actual odds of having the disease are only about 33%. The technical term for this is the “positive predictive value” of a test.
If you are unsure about the calculations, think about it this way: Imagine that we are testing 1,000 people, pulled at random from the general population. Of those 1,000 people, only 1 person is statistically likely to have HIV. Let’s presume that, for that person, the test was accurate.
However, with a 99.6% accuracy rate, the test will fail four times out of a thousand. That means that we have, on average, four false positives in our sample of 1,000 people. Which means in turn that, of the five people who tested positive, only one person actually has the disease. This is slightly different from our calculation above because, as noted, we simplified it earlier for convenience of explanation. The actual calculated value is just about one out of four.
Here’s a back-of-the-envelope way to estimate the chances: The likelihood that a positive screening test is accurate is roughly the incidence rate of the disease in the population divided by the failure rate of the test (multiply the result by 100 to get a percentage). The low failure rate for the test must be reckoned with the low incidence rate for the disease.
Let me stress, all this reckoning assumes that our only information comes from a single screening test (that is, there is no reason apart from the test to believe that you might have a given disease). Of course, as with any disease, if you do have symptoms or risk factors, that changes the picture significantly in favor of believing the test.
Medicine isn’t the only area in which we should keep Bayes’ Rule in mind. The main point is about the way we reason. Most of us naturally think that the probability of evidence, given a particular hypothesis, is the same as the probability of a hypothesis, given the evidence. As we have shown, this is not necessarily the case. The two quantities can radically diverge.
Thus, when reasoning about probability, we should recognize what the probabilities really mean. They may not mean what we conventionally assume.
Next: The philosophical controversy in which Bayes’ rule was born is still relevant today.
Notes: The illustration of Thomas Bayes, above, is the only one available. He was not a widely known figure in his lifetime and the identity is not confirmed.
If you are interested in the real world of probability, you may also enjoy these items by economics prof and statistician Gary Smith:
The paradox of luck and skill: Why did Shane Lowry win the British Open golf championship? Because someone had to. At the highest levels of competition, skill is a given and luck reigns.
and
Computers excel at finding temporary patterns. Which contributes to the replication crisis in science.
