While helping a friend’s teenage son with math, I was perusing the textbook used. I was dismayed by the presentation of the topic of translating graphs. More than that, I believe the issue reflects some general problems with how mathematics is typically presented to high school students.

Specifically, the text addressed how to do graph transformations for exponential functions. That is, if you have a function with the form y = a ⋅ b^x (where a and b are constants), how would you create a new equation whose graph was moved up, down, left, or right? The method the book proposed, while technically correct, misses a huge opportunity to help students.

The book presents a general form for transforming exponential equations. The form is y = a ⋅ b^x–h + k. Here, h is the number of units to move the equation to the right (negative for left), and k is the number of units to move the equation up (negative for down).

Now, you can use this equation perfectly well for doing simple transformations of exponential functions. The problem, though, is that it provides no context for the student to know why this is true. Sure, we trust that the authors of such books know what they are doing. But how does the book know where to put h and k in the equation? Why is h subtracted and k added? If I wanted to transform a different equation, how should I modify my equation to transform it?

Sadly, none of these questions were answered by the book. Additionally, it offered multiple different types of equations (linear, quadratic, and exponential), and gave separate equations for transforming each type of equation. That seems all well and good, but the truth is that there is only one set of rules that you need to know to transform any equation and these rules can be explained easily both in terms of what to do and why they work. Then, you don’t need separate rules for each type of equation and students understand that math is not about memorizing formulas but about learning to think about equations in new ways.

What are the rules? They are very simple and straightforward. To move an equation to the right (i.e., along the x-axis) h units, replace every instance of x in the equation with (x – h), including the parentheses. To move an equation up (i.e., along the y-axis) k units, replace every instance of y in the equation with (y − k), including the parentheses. That’s it! That’s all you need to do for any possible equation. To prove this to you, I will show you a crazy-complicated equation, and then we will apply our rules to move the graph up two units and to the right three units. The equation will be:

y³ − 5x²y⁵ = y sin(x):

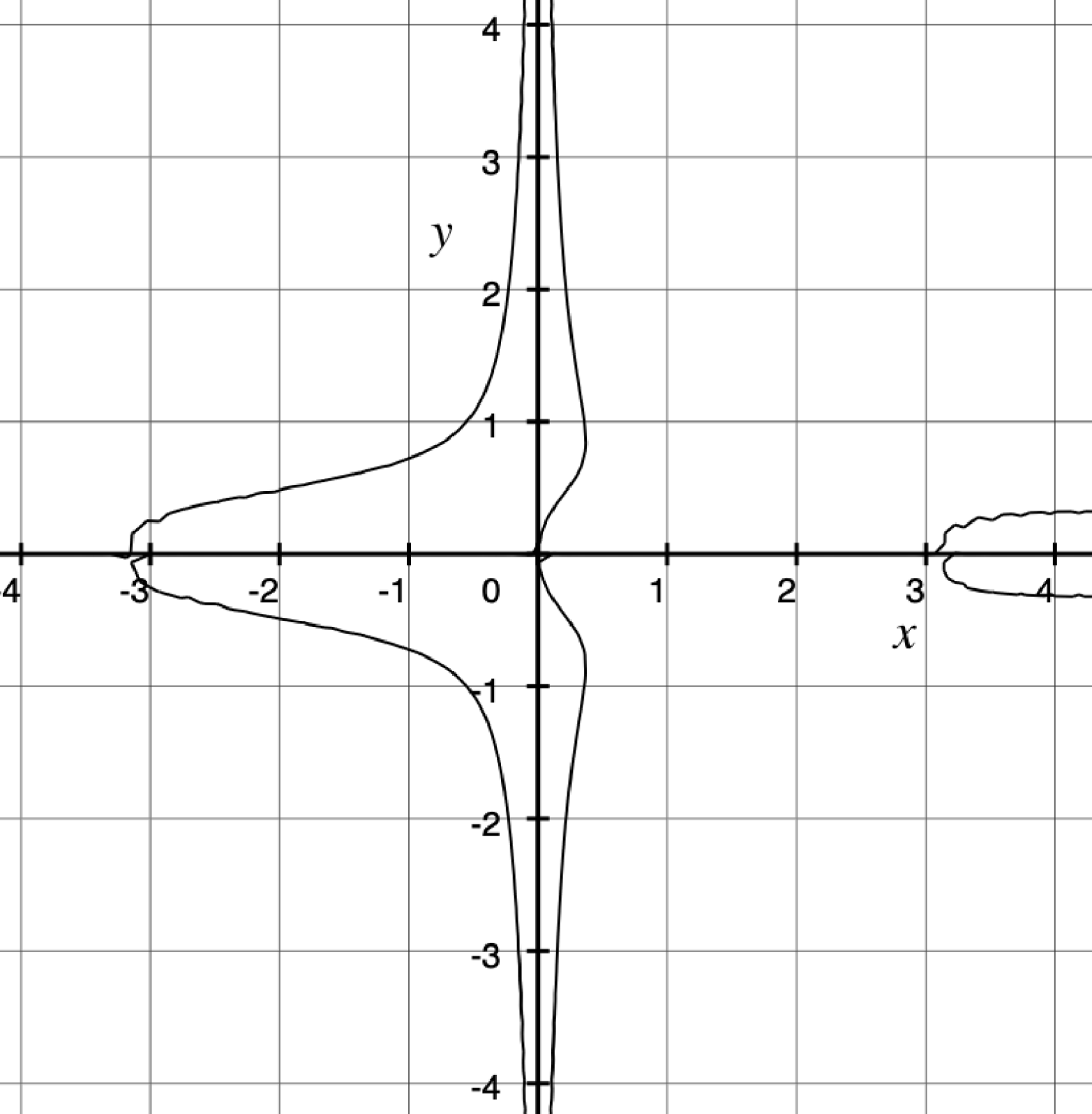
So, to move it up two units and to the right three units, we need to replace every y with and every x with (x − 3). So the new equation becomes:

(y − 2)³ − 5(x − 3)²(y − 2)⁵ = (y − 2) sin((x − 3))

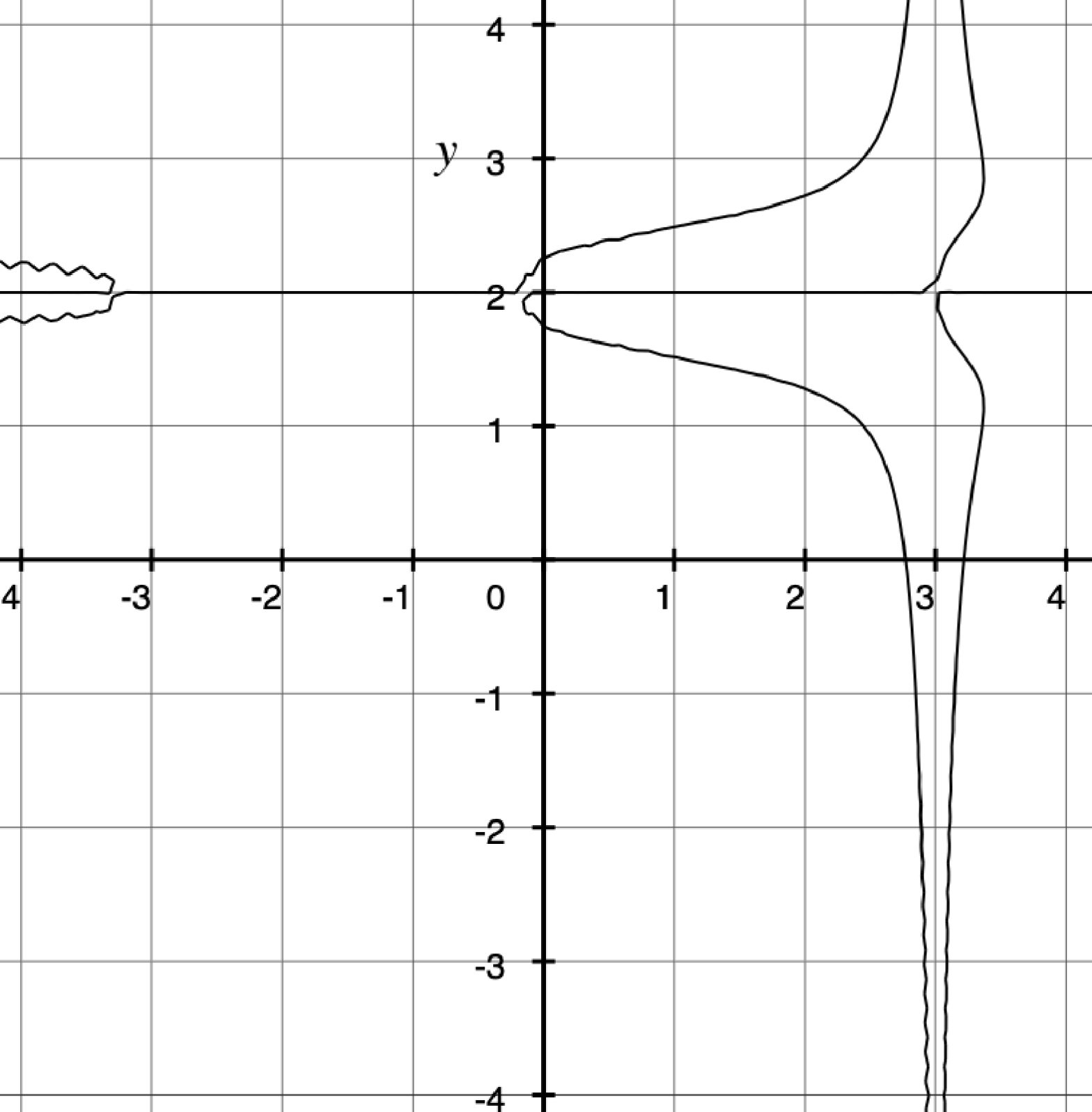
As you can see, this is the exact same graph as before, just shifted up and to the right. I was able to explain the transformation in a single sentence, and apply it to an arbitrarily complicated equation, not just one with a predefined format. Additionally, the same ideas would continue to apply even if I added variables. For instance, if I added a z variable for depth, then a similar modification to z would move the graph closer or further away.

Additionally, I can also straightforwardly tell you why this works. By replacing each instance of x with (x − 3), we are essentially telling the graph to plot the point it would have plotted if x were three units less. With the method portrayed in the book, there is no reason behind it, just something you have to do. This approach greatly disconnects students from the mathematics they are involved in. They might be able to do the work, but it leaves math forever as a mystery.

Overall, this book made two fundamental mistakes when teaching this concept. The first is that it was teaching mechanics instead of general principles. It taught students how to do something, not what the general principles are. Of course, there are times when teaching someone how to do something is appropriate — it depends on the student’s age and the specific subject. For instance, teaching the how of addition and subtraction is important because the students learning are usually younger (and therefore are better with performing concrete steps) and because the methodology is highly generic (it applies to all addition problems). Here, the situation is the opposite. The topic is being taught to older students who are at the appropriate age for learning general principles, and the “how to” part of the method being taught doesn’t generalize — it only works with one specific type of formula. In the methodology presented here, you get both a generalized how (the methodology works for any formula) as well as a simple explanation for why it works.

The second fundamental mistake is the focus on functions. A function is essentially a formula for getting a value. Don’t get me wrong, functions have an important role in mathematics. But, unfortunately, because they are widely used in proofs (they tend to make proofs easier), many mathematicians continue to focus on functions even when it isn’t appropriate. Notice the form of the original transformation equation defined by the book: y = a ⋅ b^x–h + k. In the methodology presented here, the equation would look like this: y – k = a ⋅ b ^x−h.

Even if the general formula weren’t being taught, this formulation is at least suggestive of the rule. It shows subtraction for both h and k, and doesn’t leave the student wondering why one was added and one was subtracted. However, this form isn’t the form of a function, where y is on one side, and the calculation for y using x is on the other side. It is in the more general form of a relation, where the variables are freely intermixed. Focusing too much on functions over relations leads to lower mathematical understanding and intuition.

Overall, if we want students to connect with mathematics, we should be training their mathematical intuition to help them to reason about mathematical problems, not just teaching them isolated techniques with extremely narrow applications. Students are not likely to need the isolated tricks in the real world, but the thinking skills will be helpful no matter what endeavors they choose in the long run.

Note: For a discussion of this approach in higher-level mathematics, see this interesting paper.

You may also wish to read: What do we want with mathematics curriculum? Jonathan Bartlett: If we are going to dedicate such a large portion of our children’s lives to learning mathematics, we had better know why. Knowing why we teach mathematics informs what mathematics is taught, how it is taught, and what level of understanding we should require of students. (Jonathan Bartlett)