Using Benford’s Law to Detect Bitcoin Manipulation
Market prices are not invariably equal to intrinsic valuesFor a while, there was a popular belief among finance professors that the stock market is “efficient” in the sense that stock prices are always correct — the prices that an all-knowing God would set. Thus, investors can buy any stock, even a randomly selected stock, and be confident that they are paying a fair price.
This belief was based on seemingly overwhelming evidence that changes in stock prices are difficult to predict. Efficient market enthusiasts argued that if stock prices are always correct, taking into account all currently available information, then any changes in stock prices must be due to new information which, by definition, is impossible to predict. Therefore, the evidence that changes in stock prices are hard to predict proves that the stock market is efficient.
This argument is a common fallacy. The fact that A implies B does not mean that B implies A. The fact that all of the players in the Premiere League are male does not imply that all males play in the Premier League. Here, the fact that an efficient stock market implies that stock prices are impossible to predict does not mean that if stock prices are impossible to predict then the stock market must be efficient.
Changes in stock prices may well be difficult to predict because it is impossible to predict what investors, acting on the basis of what Keynes called “animal spirits,” will do next. The periodic occurrence of speculative bubbles is ample evidence that investors are sometimes irrational and stock prices are sometimes whacky.
For example, the crazy gyrations in bitcoin prices are ample evidence that financial markets are not efficient. Since bitcoins generate no income, their intrinsic value is zero, yet people have paid hundreds, thousands, and tens of thousands of dollars for bitcoins. One explanation is that bitcoin prices have been manipulated by pump-and-dump schemes in which the unscrupulous circulate boisterous rumors while they trade bitcoin back and forth among themselves at higher and higher prices, and then sell to the naive who are lured into the market by the rumors and seemingly ever-rising prices.
One fascinating test of the pump-and-dump theory is based on a remarkable relationship known as Benford’s law. Suppose that we look at the annual profits of thousands of companies and record just the first digit of each profit number; for example, 34 would be recorded as 3, 428 would be recorded as 4; and 1793 would be recorded as 1. We might think, reasonably enough, that each digit, 1 to 9, would appear about the same number of times. Benford’s law, however, predicts that 1 is more likely than 2, that 2 is more likely than 3, and so on, as shown in Table 1. It is 6.5 times more likely that the leading digit will be 1 than 9.
Table 1 Benford’s Law
Leading Digit Probability
1 .301
2 .176
3 .125
4 .097
5 .079
6 .067
7 .058
8 .051
9 .046
This puzzling relationship was reportedly discovered in the 1880s by a mathematics professor named Simon Newcomb. Before computers and the internet, people looked up logarithms in books containing table after table of logarithmic values. Newcomb noticed that the early pages were dirtier and more worn than the later pages, leading him to speculate that numbers that begin with 1 are more common than other digits.
In the 1930s a physicist named Frank Benford tabulated the leading digits of all sorts of data and confirmed that 1 was the most common number, with the frequencies declining roughly as shown in Table 1. Soon there were mathematical proofs of situations in which Benford’s law holds. For example, the distribution of leading digits of the product of randomly chosen numbers follows Benford’s law.
One way to think about this law is to compare the distance from 1 to 2 with the distance from 2 to 3. If we are adding numbers together, the distances are both equal to 1. If we are multiplying numbers, however, then we are dealing with percentage increases, and the distance from 1 to 2 is 100 percent while the distance from 2 to 3 is only 50 percent—which means that going from 1 to 2 is less likely than going from 2 to 3; going from 2 to 3 is less likely than going from 3 to 4; and so on. Therefore, a number initially in the interval 1 to 2 is more likely to stay in that interval than is a number initially in the interval 2 to 3. The same argument applies when we compare the intervals 10-20 with 20-30, when we compare 100-200 with 200-300, and so on.
For example, if we compare the price of a company’s stock one day and the price several days later, the price several days later is determined by the product of the daily percentage changes and, so, is governed by Benford’s law. To test this, I looked at the prices of all stocks traded on the New York Stock Exchange (NYSE) on July 6, 2021. For 29.1 percent of the stocks, the leading digit was 1, which is close to the 30.1 percent implied by Benford’s law. The number 9 was the leading digit for only 4.8 percent of the stocks, which is close to the 4.6 percent implied by Benford’s Law. Figure 1 shows the full theoretical and empirical distributions. The close correspondence is striking for such a relatively small data set.
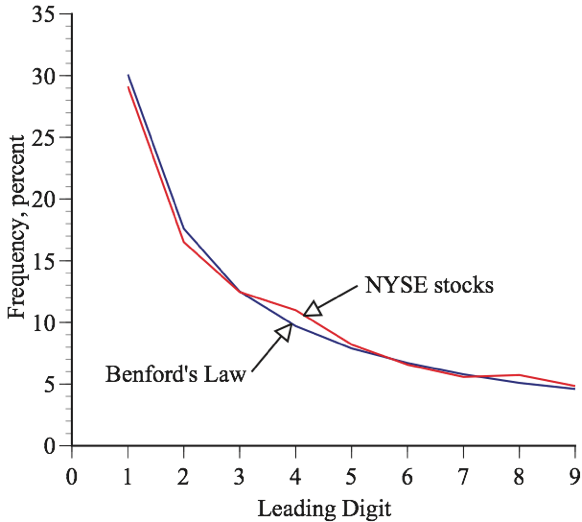
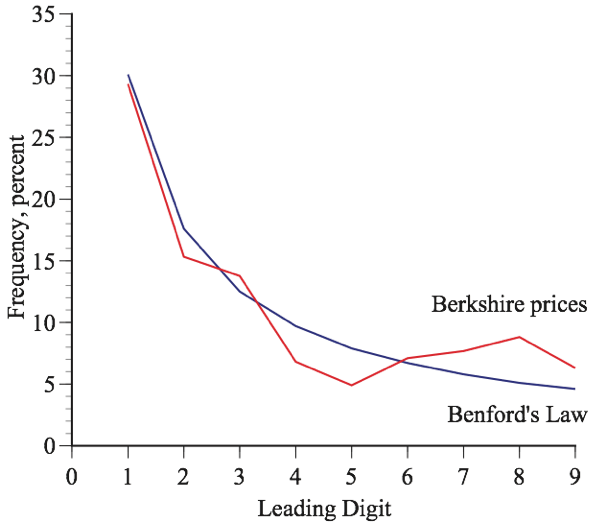
Figure 2 compares the distribution of the leading digits of the price of Berkshire Hathaway stock since 1980. Again, the fit is not perfect but reasonably close.
Benford’s law is more than just a surprising relationship; it can also be used to detect fraud. When people make up data, it is tempting to assume that, to avoid detection, the numbers should “look” random with every digit showing up equally often and no suspicious patterns, like five 1s in a row. However, if it is a situation where Benford’s law holds, there should be more 1s than 2s, more 2s than 3s, and so on.
Since a company’s revenue, costs, profits, and other measures of financial performance are likely to grow over time by percentages, they should be governed by Benford’s law. Thus, Benford’s law can and has been used to identify accounting fraud.
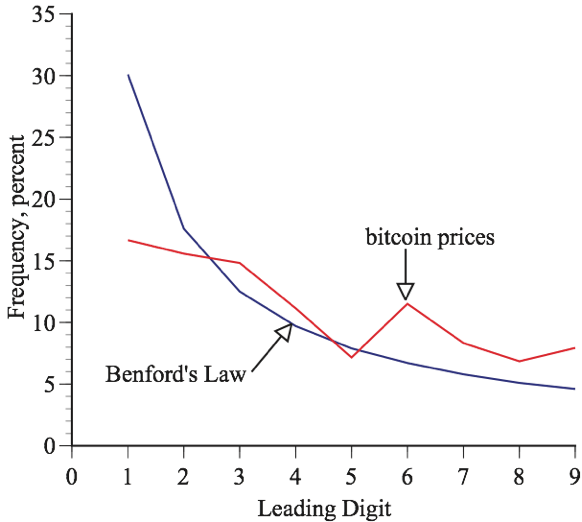
It can also be used to detect fraudulent bitcoin trades — so-called wash sales where a group of conspirators trade bitcoin back and forth among themselves at ever higher prices. Since increases in bitcoin prices are likely to be multiplicative, they should be governed by Benford’s law. They are not. Figure 2 show the distribution of the leading digits of daily bitcoin prices back to 2014. Small digits appeared somewhat more often than large digits, but not nearly as often as implied by Benford’s law.
The market manipulation, the irrational price gyrations, and the enthusiasm of so many investors for investing in bitcoin (and other cryptocurrencies) is ample evidence that market prices are not invariably equal to intrinsic values.
Benford’s law is one of those cases where an empirical observation was the inspiration for a theory that turned out to be validated. If a computer data-mining algorithm had discovered this mysterious pattern, the algorithm would have no way of figuring out the conditions under which it is likely to be true. Humans could and did. Nor would a computer algorithm recognize how and why Benford’s law could be used for fraud detection. Humans could and did.
