The Needless Complexity of Modern Calculus
How 18th century mathematicians complicated calculus to avoid the criticisms of a bishopCalculus often sends chills up the spines of students. Even the word itself incites panic in undergraduates everywhere. Would you be surprised if I told you that the essentials of calculus are actually very straightforward and simple? In fact, they are so simple that most people with a modest Algebra background can understand calculus easily.
So why do students think it is so scary? The fact is, calculus is taught in such a convoluted way that the natural beauty of it is almost always greatly distorted. Why? Because an 18th century bishop made fun of calculus professors. Seriously. We’ll get to the “why” towards the end of the article.
To understand the simplicity and beauty of calculus, I am going to teach you some. Calculus is split into two parts, “differential calculus” and “integral calculus,” which are just opposites of each other, much the same way that addition and subtraction are opposites of each other and multiplication and division are opposites of each other. We will focus on differential calculus here.
Let’s take an equation: y = x2 + x. This equation makes the graph below:
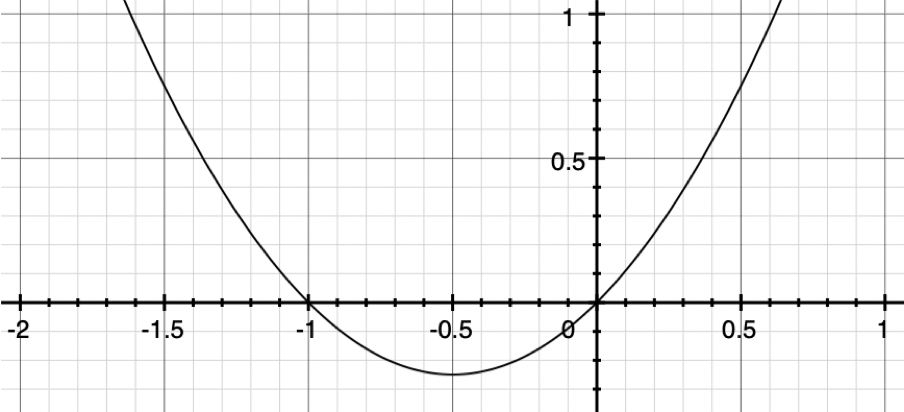
While algebra studies the relationships between the values in an equation (i.e., what is y when x is a particular number), calculus is the study of the relative changes of those same variables. So, as x changes, how much does y change as a result? This is why it is called “differential calculus,” because we are looking at how the changes (i.e., the differences) behave. However, calculus doesn’t measure large changes. Actually, calculus only measures extremely small changes. In fact, these changes are so small that they are infinitely small and are known as infinitesimal changes, or just infinitesimals.
There is a simple technique that can be applied to study infinitesimals. For every variable in the equation, we will create a second variable that represents a change in that variable, and put a “d” in front of it. So, if we have the variable x, the change in that variable will be represented by dx. If we have the variable y, the change in that variable will be represented by dy. This is NOT “d times x”, but a single quantity dx represented by two letters. This is known as the “differential of x” or just pronounced as “dee ex”. This is the infinitesimal amount that x changes, and dy is the infinitesimal amount that y changes correspondingly.
Now, all you have to do to discover an equation relating the variables and their infinitesimal changes is simply replace every instance of the variable with the variable plus its change. So, every x will become (x + dx) and every y will become (y + dy). The parentheses are important, because otherwise you might wind up making order-of-operations errors.
So, we can take the equation above and perform the replacements.
We start with
y = x2 + x
and transform it to
(y + dy) = (x + dx)2 + (x + dx)
If you remember your algebra, you can simplify it as follows:
y + dy = x2 + 2x dx + dx2 + x + dx
If you subtract the original equation from both sides you get
dy = 2x dx + dx2 + dx
One other notion in calculus is that, if you multiply two differentials (or raise a single differential to a power), they can essentially be treated as non-existent. If one differential is infinitely small, then two of them multiplied together you can think of as another order of infinity smaller. Therefore, they can be essentially treated as non-existent. Therefore, we can say that dx2 is just too small to be worth considering and can be dropped. This leaves us with
dy = 2x dx + dx
So what can we do with this? Well, the slope of the graph at any given point is given by the relative changes in y and x at that particular point. Since dy and dx represent infinitely small relative changes, then their ratio represents the slope at a particular point. Therefore, if we solve for dy/dx, then we will know the slope at any given point. This can be done by dividing both sides of the equation by dx. This gives
dy/dx = 2x + 1
So, at any point on the graph, the slope will be two times the x value plus one. You can see the slope of the graph at x = 0.25 below:
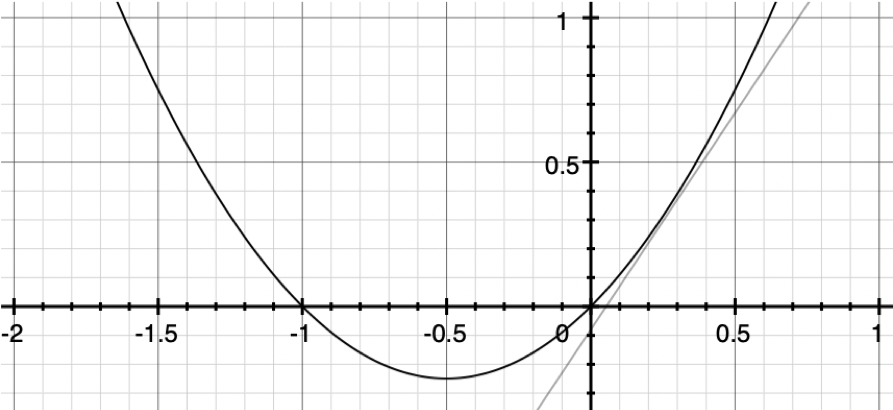
Here, the slope is 1.5, which means that the slope is going up when moving from left to right.
Now, while that may seem straightforward, it actually takes most calculus courses a full half-semester to explain that concept. While I did take a few shortcuts, it certainly doesn’t take weeks and weeks of classes to explain it.
Why does it take an average class that long to master these concepts? Modern calculus is buried in an avalanche of 19th century mathematics that arose because an 18th century bishop made fun of atheist mathematicians, and those mathematicians worked long and hard to make sure that the barb didn’t stick.
George Berkeley was a bishop, a philosopher, and a mathematician. He wrote a book titled The Analyst. But, it wasn’t the title that made mathematicians flinch. It was the subtitle. The subtitle of his book was “A Discourse Addressed to an Infidel Mathematician: Wherein It Is Examined Whether the Object, Principles, and Inferences of the Modern Analysis Are More Distinctly Conceived, or More Evidently Deduced, Than Religious Mysteries and Points of Faith.”
You see, Berkeley had noticed that infinitesimals were very odd beasts indeed. Though they were inestimably useful, they were hard to really define well, especially in material terms. Berkeley picked up on this, and he pushed this line of thinking forcibly. He taunted the mathematicians of his day, saying, “And what are these same [infinitesimals]? They are neither finite Quantities nor Quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?” He then laid down the gauntlet. “He who can digest … a second or third [infinitesimal], need not, we think, be squeamish about any point of divinity.”
While not every criticism made by The Analyst was accurate, this line of accusation struck a nerve with many mathematicians (even religious ones) who viewed themselves as finding truth in a more objective way than that of religion. Some mathematicians were so offended by the implication that they set off a quest to figure out how to do calculus without mentioning or referring to infinitesimals in any way.
In fact, in the two years following publication of The Analyst, four books came out to show that calculus can be done without infinitesimals, which is more calculus books than had been published in the previous thirty years.
To some extent they were successful. It is possible to do calculus without infinitesimals. But doing so transforms calculus from a simple, straightforward application of algebra to infinitesimals into a murky mess of arcane and esoteric theorems and axioms. Rather than feeling like a natural extension to algebra, learning calculus the modern way feels like learning an alien language.
If you wondered why calculus feels so complicated, now you know—it’s because 18th century mathematicians didn’t appreciate the comparisons to religion. But perhaps our students would appreciate it if math classes were taught in the way that made the most sense, not with needless complexity added to skirt religious intonations.
For readers wanting a more nuanced history of this subject (yet still quite intriguing), one should look at Florian Cajori’s A History of the Conceptions of Limits and Fluxions in Great Britain: From Newton to Woodhouse, available at the Internet Archive.
