(Recently, we’ve been asking readers to think about Alice and Bob, the famous pair in physics used to demonstrate propositions in a variety of contexts but we began to focus on what happens if Alice and Bob are competing for a political office. Bernard Fickser, whose argument for reform we have been following, offers a look at how a crypto secure election system might work.)

We now come to the most interesting part of this article, namely, a cryptographically based protocol for securing elections. If such a protocol can be made to fly, it will do much to secure free and fair elections as well as to boost voter confidence that votes are being accurately counted and not mixed with fraudulent votes. I want in this section to argue that the tools of cryptography actually do allow for such a protocol. I will lay it out briefly, yet in sufficient detail, to (hopefully) convince readers of its feasibility.

5.1 The “Un”necessity of Dedicated Voting Machines

First off, the Cryptosecure Election Protocol (or CEP) will be formulated independently of any dedicated voting machine. It is really quite remarkable, and even ridiculous, that elections should use and depend on dedicated hardware devices that run proprietary black-box algorithms (protected by patents no less). It’s like creating a market for horse and buggy when Tesla electric vehicles exist.

To understand why dedicated voting machines should be a thing of the past, consider that we live in an age of smartphones, which by the standards of 25 years ago (given Moore’s Law) are supercomputers. These smartphones are all-purpose computers. We no longer need to buy a separate metronome, a separate mp3 player, a separate video recorder, a separate stopwatch, etc. With the right apps, smartphones are all-in-one computational devices. So are current laptop and desktop computers.

Smartphones illustrate what may be called “the Turing Principle,” after the key figure in modern computing, Alan Turing. Usually, in computer science, this principle is called the Turing Thesis (or the Church-Turing Thesis, giving additional credit to the logician Alonzo Church, Turing’s dissertation supervisor). The Turing Thesis states that all computation can be done with a few very simple algorithmic building blocks, such as addition, subtraction, instructions for changing memory locations, and conditional transfers of control (i.e., if this, do that, otherwise do something else).

The Turing Principle is a bit less formal than the Turing Thesis. It’s point is that all working computers are essentially the same and that, in practice, the only difference is speed and memory. So, with regard to elections, the implication of the Turing Principle is that there’s no need for uniquely purposed hardware or software (such as Dominion Voting Systems) to keep track of votes.

5.2 Structure vs. Function

Instead, and this is crucial, what’s needed for a credible voting system is for any hardware and software used in voting to perform certain verifiable functions, regardless of the underlying hardware and software used. It’s the classic distinction between structure and function. Voting machine companies provide structures—actual hardwired machines and particular proprietary algorithms that run on them. What we need are verifiable functions—things that machines, regardless of underlying structure, can do, and in ways that we can verify.

So let’s get started with the CEP. Given the 2020 U.S. presidential election, in which ballots took many different forms, and where show-up-in-person voting played a diminished role because of widespread mail-in ballots, the CEP will be formulated for purely digital ballots. This, it seems, is in fact the future of voting. Interestingly, it also allows for more secure elections than going non-digital.

Those who witnessed the transition from typewriters to word processors in the 1980s will remember the resistance to digital documents, which were at the time treated as less securely preserved than paper documents. But in the end, we’ve come to regard the digital as more secure, capable of being housed in multiple virtual locations, being immune to fire, loss, and degradation, and being readily searchable.

Digital ballots promise a similar advantage over paper ballots. The CEP can accommodate a hybrid approach that also uses paper ballots but only by digitizing the paper ballots and thereafter treating them the same as ballots that were digital from the start. Despite this possible flexibility, we’ll be purists here and develop the CEP for purely digital ballots.

5.3 Alice’s and Bob’s Ledger of Votes

Our example election is between Alice and Bob (for simplicity, let’s assume no other candidates and no other offices are up for election thoughgeneralizing to more candidates and offices is straightforward). So there is Alice’s ledger of votes in her favor and Bob’s ledger of votes in his favor. The election commission can set up a website for the election, let us say at alice-v-bob-election.gov. Alice’s ledger of votes can then be recorded at alice-v-bob-election.gov/alice and Bob’s at alice-v-bob-election.gov/bob.

These two ledgers can be updated in real time. Poll monitoring organizations, especially those sponsored by the political parties to which Alice and Bob belong, will monitor these sites and use data integrity methods (notably hashing and blockchains) to ensure that any changes at any given point in the election are made to ledgers whose integrity has been confirmed up to that point. Ensuring data integrity in this way is well-worn ground, and here’s no need to rehearse it here.

On a side note, even without formal cryptographically-based data integrity methods, internet users have invented a virtual equivalent through caching and screenshots of web content. For instance, if someone posts something on Twitter and then removes it, or if someone posts something on a blog and then revises it to remove an embarrassing detail, because Internet users are constantly caching and taking screen shots of online content, it’s virtually impossible to remove or deny anything that has appeared online. Data integrity methods simply make the process of verifying and preserving digital content more formal and foolproof.

5.4 The Ledger of Registered Voters

The ledger of registered voters needs to be considered next and can reside at alice-v-bob-election.gov/registered-voters. This ledger gets updated in real time, so, as with alice-v-bob-election.gov/alice and alice-v-bob-election.gov/bob, the ledgers of Alice and Bob, the ledger of registered voters will likewise be monitored and preserved using data integrity methods.

In building the ledger of registered voters, we start with a ledger of eligible voters, say, at alice-v-bob-election.gov/eligible-voters. Though it (and the other ledgers) will actually be a relational database, we can imagine it as a giant online spreadsheet with first name, middle name, last name, and alternate names in different columns, each row corresponding to a single eligible voter. Other voter information (address, age, etc.) may need to be present to disambiguate names (how many eligible voters have the name “John Paul Smith”?).

5.4.1 Proof of Identity

To be a registered voter, and thus have one’s name moved from the ledger of eligible voters at alice-v-bob-election.gov/eligible-voters to the ledger of registered voters at alice-v-bob-election.gov/registered-voters is going to require proof of identity (PoI). Thus, it’s going to be up to the election commission to gather such PoI information and up to each voter to supply it. There has to be a collaboration here. To be a registered voter is more than simply being an eligible voter and requires some act or effort that clearly identifies and thereby authorizes a voter to vote in the election between Alice and Bob.

Security and privacy concerns now become important and will need to balance each other. Imagine, for instance, a voter comes into the election commission offices and identifies him- or herself as a particular voter. The election commission can attempt to confirm the voter’s identity by asking for a state-approved photo ID. But it could go much further. It could ask for biometric authentication and identification, everything from fingerprints to retinal scans to gait analysis. Asking for a state-approved photo ID seems pretty minimal. Asking for full-fledged biometric data seems a bit much.

The entire procedure for gathering Proof of Identity (PoI) data and thus registering a voter could conceivably be put online. For instance, in some states it’s possible to apply for one’s birth certificate online by answering certain challenge questions about one’s life and activities (state and federal government seems to track our movements quite precisely and know the “right questions” to ask). This information plus a payment by bank draft or credit card can be enough to secure a valid birth certificate.

Whatever the information used to establish PoI and however it is gathered, it will need to be captured digitally. Thus, if a photo ID is used, a digital scan of it will need to be preserved. If biometric data are used, they will need to be preserved, perhaps via digital video. Likewise with any other information used to establish PoI. So, for a given name N taken from the ledger of eligible voters, there will be a data file Z (it can be a lossless compression ZIP file) that contains all such evidence establishing proof of identity (PoI).

The data Z allows for the name N to be moved from the ledger of eligible voters to the ledger of registered voters. Yet because the list of registered voters is publicly visible at alice-v-bob-election.gov/registered-voters, confidentiality requires that the information in Z be hidden from the public. To that end, the election commission will put next to the name N not the PoI data Z itself, but a hash of it, i.e., hash(Z). Because Z is N’s data as much as, and indeed more so than, the election commission’s, both N and the election commission will have full access to Z. Both will keep it confidential, yet both can make it available as needed.

Hash functions are widely known and used, especially in cybersecurity. They are one-way functions, which is to say they are easy to compute but hard to invert. Hash(Z) can therefore be quickly calculated, yet it is virtually impossible (i.e., with extremely low probability) to reverse it and find what data returned a given hash value simply from that value. (In fact, hash functions tend to compress information, even reducing megabytes to a few hundred bits, so technically speaking the challenge is not to invert them but to find a preimage that maps onto a given hash value.)

So, if someone sees hash(Z) but doesn’t know that it came from Z, there’s no way for this person to determine Z. And yet, if someone tries to tamper with Z and say that instead the PoI information for N was not Z but instead W, it will be instantly clear that this can’t be so because hash(W) will, with overwhelming probability, not equal hash(Z). Data that is very similar, that differs even in only one place, will yield extremely different hash values. Hash functions are extremely discontinuous, so data that look very similar (perhaps differing in only a single bit) will yield completely different hash values.

A common hash function is the Secure Hash Algorithm created by the National Security Agency and distributed by the National Institute of Standards and Technology. It happens also to be the hash function used by Bitcoin. SHA-256 maps arbitrary strings to strings of 256 bits, or 64 characters in hexadecimal notation. It’s easy to find SHA-256 calculators online (here’s one).

5.4.2 The Worry of Technology Overload

I want to step back for a moment and consider the worry of “technology overload” on the average voter N. For instance, am I, in proposing the CEP (Cryptosecure Election Protocol) really expecting voters to find an SHA-256 calculator and use it to compute the hash of their PoI data Z? Yes and no. No, in the sense that voters will not need to know any of the nuts and bolts of these technologies, but Yes in the sense that via convenient apps (actually, a single app could handle the entire CEP), voters will nonetheless be performing the underlying functions. Apps can readily compute SHA-256, and the hash values computed can be readily stored as QR codes or other matrix barcodes.

Because the CEP depends entirely on the performance of verifiable functions, any apps that voters use will be interchangeable with other apps that perform the same function. If a voter belongs to a particular political party, it will be likely that the party will supply such apps to its members. To avoid false flag recruitments, however, it may be advisable to go with independent third parties, especially those that guarantee privacy and the absence of user tracking.

5.5 Two Public-Private Cryptographic Key Pairs (Four Keys Total)

To round out the protocol, the voter N will now need to generate two public-private key combinations (E,D) and (E’,D’) with respect to a reliable public-key cryptosystem. E and E’ represent the encryption keys of a public-key cryptosystem, D and D’ respectively the decryption keys. In public key cryptography, the public is given an encryption key, so that it can encrypt messages at will, but decryption requires also knowing the decryption key, which is kept private to the user generating the key combination.

As the Wikipedia article on public-key cryptography explains in the caption to the following diagram, in an asymmetric or public-key “encryption scheme, anyone can encrypt messages using the public key, but only the holder of the paired private key can decrypt. Security depends on the secrecy of the private key.”

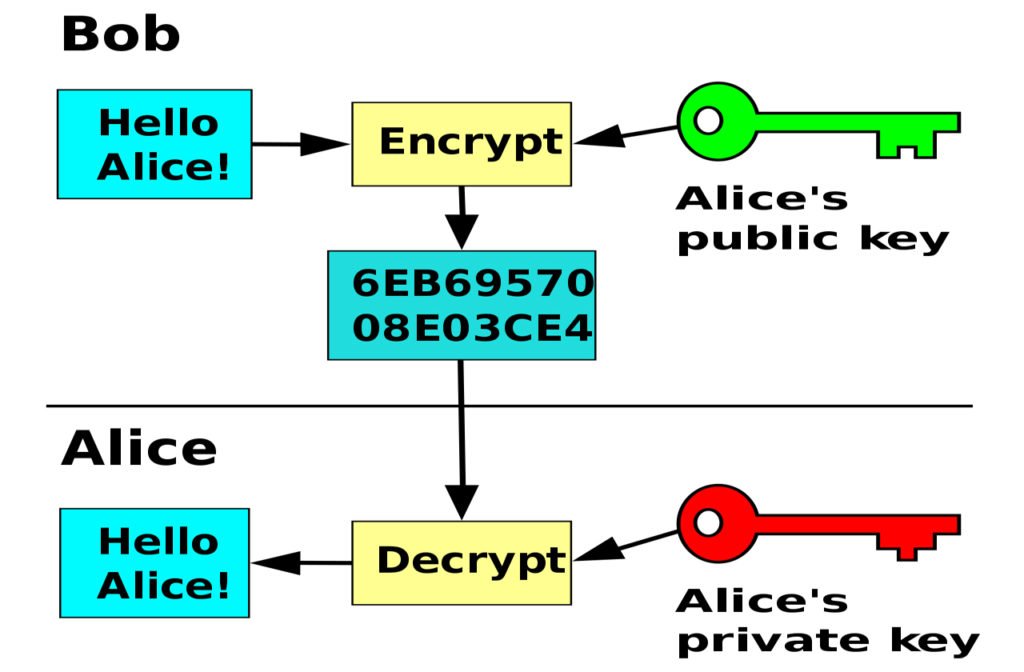
For our purposes in the CEP, RSA (Rivest-Shamir-Adleman) public key cryptography would be fine, but so would DSA (Digital Signature Algorithm) or ECDSA (Elliptic Curve Digital Signature Algorithm).

Why is a voter N going to need two public-private key combinations (E,D) and (E’,D’)? The reason is that voters, in order to vote in secret, need to separate their identity from their ballots in dealing with the public and with the election commission. This means there needs to be a way for voters to ensure that their ballots are duly recorded (hence one public-private key pair) and that they can identify their ballots even if others can’t (hence the need for another pair). Moreover, voters will need to be able to prove to others that their votes did or did not get adequately counted. Public-key cryptography, used with two key pairs protects voter confidentiality and assures voters that their votes are properly counted. Again, it’s all about the voter.

For convenience, let’s now imagine that the voter N has email address N@gmail.com and cell number 555-555-5555. This information can be included in the PoI data that N provides to the election commission. In addition, the PoI data needs to include E (from the public-private key combo (E,D)) and a hash of D’, i.e., hash(D’) (from the public-private key combo (E’,D’)). By hashing the private key D’, N effectively hides D’ from others but can reveal knowledge of D’ to others by, if needs be, revealing D’ and showing that it does indeed equal the value previously assigned to hash(D’). All this information is then incorporated into the PoI data file Z.

The election commission then securely emails Z as an attachment to N@gmail.com (perhaps with two-step verification using N’s cell number before hitting “send”). Next to N’s name at alice-v-bob-election.gov/registered-voters, the election commission now puts hash(Z). And N, with an app that computes the hash function, confirms that the attachment sent to N@gmail.com has a hash that indeed computes to hash(Z) as on the server.

Such confirmations can be quickly accomplished with QR barcodes (the “QR,” after all, refers to “quick response”). If at any point what’s appearing on the election commission’s server does not agree with what N thinks should be there, N, or a third-party representative, can challenge the election commission and prove (this is the crucial point) that the election commission’s data has been compromised. Yet because compromises to data integrity can be so easily uncovered, we can expect the election commission to be incentivized to keep such incongruities to a minimum.

5.6 Securing Against Loss of PoI Data

So far the data recorded next to N’s name at alice-v-bob-election.gov/registered-voters looks like . This voter array needs to be expanded. It needs to be clear that the election commission is preserving, as in backing up, the PoI data that makes up Z. The problem is that hash(Z) comprises only a few bits of information (256 with SHA-256), so for big zip files Z, it will be impossible to reconstruct Z simply from the hash value hash(Z), and that would be true even if the the hash function were readily invertible (which it is not).

Granted, N is supposed to keep a copy of Z. But if there is identity fraud in which the election commission itself or other bad actors are attempting to create voters out of thin air, it’s going to be important for independent parties to be able to examine the actual PoI data for each supposed voter. The election commission therefore needs to preserve Z and not be able to claim that Z was lost. To that end, N’s voter array should also include encrypt(Z), namely, a lossless encryption of Z by the election commission, which it makes public, which it can decrypt at will or be ordered to decrypt by a court, and which will prevent it from losing or claiming to have lost Z.

5.7 Rounding Out the Voter Array

In addition to encrypt(Z), the voter array for N also needs to include E, the public key of the public-private key pair (E,D), and hash(D’), a hash of the private key of the public-private key pair (E’,D’). So the entire voter array for N at alice-v-bob-election.gov/registered-voters will look like . Because Z will always be unique for a given voter N and because large-scale randomization is used to choose public and private cryptographic keys (especially because these keys are generated by enlisting combinatorial explosion), all entries in these voter arrays will (with overwhelming probability) be unique, with no overlap from one voter to the next.

A voter array, as a 5-tuple, may seem a bit complicated, but it is necessary. It is also easily managed through online databases and user apps. The dominant theme in the Cryptosecure Election Protocol is the primacy of the voter. All the data associated with a given voter in an election belongs to that voter, and it must be possible for the voter to confirm the accuracy of the data. The PoI data for N, therefore, does not belong, in the first instance, to the election commission. The election commission is the trustee of the data. But because not all trustees are trustworthy, the voter needs at every point to be able to verify that the election commission is doing its job. The CEP is all about the voter, eliminating the need for trust and empowering the ability to verify.

Before moving to the ledger of ballots and how votes are actually assigned, I need to address a concern just touched on, namely, creating registered voters and their voter arrays out of thin air. For actual voters N who are able to get their voter arrays reliably positioned at alice-v-bob-election.gov/registered-voters, their votes will, as we shall see, be secure. The worry, however, is that bad actors will simply create new voters from thin air or else set up voter arrays for eligible voters who are either not planning to vote at all or planning to get registered and to vote at a later date but then find themselves already registered under a proof of identity that they did not authorize.

For voters who find themselves already registered under another PoI with public and private keys not of their choosing, they will need, and presumably have, substantial recourse to challenge the election commission (as in other cases of identity fraud involving trusted third parties). More worrisome are the voters created out of thin air (or exhumed from the grave) and those who never vote but have their identities co-opted and then are made to vote, presumably for the candidate chosen by the bad actors guilty of creating these novel voter identities.

Fortunately, because the proof-of-identity data Z is cited in the voter arrays and can be reconstructed on demand (perhaps by a court order), it will be possible to scrutinize such data and find irregularities that call into question any ballots fraudulently created by forging identities. Challenging bogus listings in the ledger of registered voters becomes evidentially stronger if the actual voters supposedly responsible for them can be located and these voters can confirm that the listings are indeed bogus. Otherwise, the evidence that there was fraud will be more circumstantial.

5.8 The Ledger of Ballots

Let’s now turn to the ledger of ballots. The ledger of ballots can be housed on the election server here: alice-v-bob-election.gov/ballots. For N to cast a ballot will require two steps or, technically, two uploads. These uploads can occur at

alice-v-bob-election.gov/ballots/ballot-upload and
alice-v-bob-election.gov/ballots/key-upload
We can imagine the ballot to be a pdf fillable form with a box next to Alice’s name and one next to Bob’s name. N will check one and only one of the boxes (in fact, as a fillable form, the possibility of checking two boxes should be precluded). In addition, N will add what’s called a cryptographic nonce to the form, some field that will hold a substantial novel random number, perhaps 50 to 100 digits, or more. The nonce helps ensure that ballots, all of which will be encrypted, don’t all encrypt just two digital ballot files (one with Alice’s name checked, one with Bob’s name checked), thus safeguarding against preimage attacks that depend on knowing details about the data that was encrypted.

5.8.1 Uploading an Encrypted (or Reverse-Encrypted) Ballot

Given a ballot V (N’s voting ballot), N now encrypts it using not the encryption key E’ but its corresponding decryption key D’, i.e., D'(V). Applying decryption in this way is a common way of cryptographically signing a digital file, such as V, and shows to anyone who applies E’ to D'(V) (= E'(D'(V)) = V), thereby recovering V, that the person who knows D’ did indeed form D'(V). Note that first decrypting and then encrypting cryptographically parallels first encrypting and then decrypting and returns intact the thing we started with.

N now performs two uploads. At alice-v-bob-election.gov/ballots/ballot-upload, N uploads D'(V). To authorize the upload, N is presented with a challenge question, namely, to decrypt some text T that was encrypted with the public key E (not E’) to form E(T). By decrypting E(T) using D, N proves to the election commission (or its servers) that it really is N on the line. This approach would require varying T, presumably randomly, from voter to voter.

An alternative approach would be to fix T and have the N compute D(T) so that when the E is applied to it, T is returned (i.e., E(D(T)) = T). Either approach can be made to work, confirming that N is on the line and thereby authorizing N to upload D'(V). The role of the public-private key (E,D) is therefore purely to confirm N’s identity and thus to authorize N to upload a ballot and thereby vote.

Once D'(V) is uploaded, it immediately appears at alice-v-bob-election.gov/ballots, and N’s voter array at alice-v-bob-election.gov/registered-voters is marked as having voted, i.e., . N will be able to confirm that D'(V) was indeed just uploaded, perhaps by using QR barcodes.

The election commission, if unscrupulous, could attach some sort of tracking pixel to D'(V) to connect this ballot with the voter N (who had to use E, and thereby divulge his or her identity, to upload D'(V)). But any such pixel will be extraneous to D'(V) and, because elections are supposed to be conducted by secret ballot, would be strongly proscribed, even by law. D'(V), because it is encrypted (or, if you will, reverse encrypted, or “cryptographically signed” by N) will by itself offer no insight into who received a vote from this ballot, whether Alice or Bob. D'(V) will therefore, immediately after its upload, reside as a yet-to-be-counted ballot at alice-v-bob-election.gov/ballots, awaiting further instructions from N before it can actually be counted.

5.8.2 Uploading the Public Key

For the encrypted ballot D'(V) to be counted, N therefore needs to do one more thing, namely upload the public key E’ (not E) at alice-v-bob-election.gov/ballots/key-upload. N will do this anonymously. All N needs to do is get E’ loaded and visible at this location on the server. Again, QR barcodes can simplify confirming that E’ has been indeed uploaded.

The election commission will want to avoid spamming and denial of service attacks, so uploading public keys at alice-v-bob-election.gov/ballots/key-upload will require some mechanisms to slow down the number of uploads, such as safeguards against robots and marking some boxes guaranteeing that the person uploading the key is qualified to vote in the election between Alice and Bob.

In fact, it doesn’t much matter how many extraneous keys are uploaded so long as it’s not too much as to overwhelm the server. Voters might even be given special access codes, not specific to particular voters, but still enough to block the efforts of bad actors to interfere in the election by uploading too many extraneous keys that would serve no role in the actual ballot counting except as spam or denial of service.

5.9 Trying All the Keys on All the Locks

So what happens when not only N but all voters like N, in two separate uploads each, upload their reverse-encrypted ballot D'(V) and the public key E’. Each voter N will be able to confirm that both D'(V) and E’ are listed on the ballot server alice-v-bob-election.gov/ballots. Essentially what we have then is a two-dimensional array of reverse-encrypted (but therefore still encrypted) ballots down one side of the array and all the public keys (perhaps with extraneous ones) down the other.

Here’s a crude diagram to illustrate the point. We imagine seven voters, “a” through “g,” that cast ballots Va through Vg by signing or reverse encrypting them with private keys D’a through D’g. And we further imagine seven public keys E’1 through E’7. The boxes in the two-dimensional array or grid then represent possible combinations of cryptographically signed ballots and public keys, and the asterisks represent where a public key E’ unlocks a ballot D'(V):

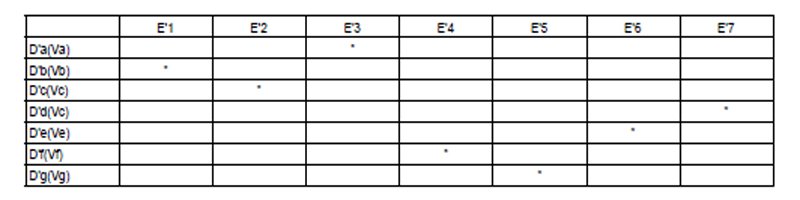
Each public key will unlock at most one reverse-encrypted ballot. If N is a legitimate voter who has followed the protocol, the composition of E’ and D'(V) will reveal V, and thus a vote for either Alice or Bob. Indeed, for any place in the two-dimensional array where E’ and D'(V) match up, it will be clear that a vote was cast and how it was cast. This vote will register either in Alice’s ledger of votes or Bob’s, and the mapping between the ballot ledger and the ledgers of counted votes will be clear.

This double uploading approach to ballots keeps the identity of the voters responsible for the ballots secure by having voters upload all their keys into one communal bin, as it were, and all the locks into another communal bin. It’s then up to the server to try all the keys on all the locks. Whenever a key opens a lock, a vote is cast.

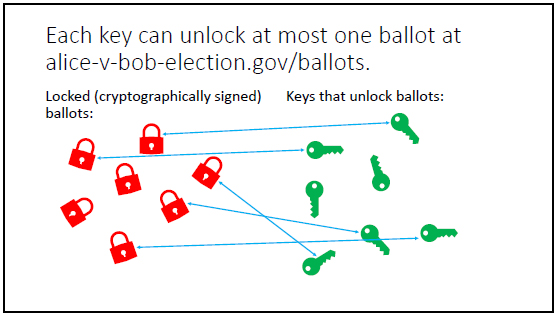
More importantly to the voter, it’s verifiable to the voter that the voter’s actual ballot contributed a vote to the candidate of the voter’s choice. That’s because voter’s will be able to identify exact their ballots of the form D'(V) as well as their public keys E’ on the ledger of ballots — they will be clearly visible to the voters who uploaded them. This approach to trying all keys in all locks is eminently computable, with the computational complexity growing not just polynomially but even quadratically in the size of the problem. Elections with hundred of millions of voters can readily be handled with this approach. (See slide handout.)

5.10 An Important Asymmetry

In the Cryptosecure Election Protocol, an important asymmetry exists between, on the one hand, legitimate voters tracking their ballots and seeing that they are actually counted and, on the other hand, legitimate voters or other responsible third parties preventing bogus ballots from being counted. With the CEP, voters are easily able to confirm their own votes, but without the voter or party responsible for a vote available, it becomes more difficult to disconfirm a vote.

Here’s how this asymmetry plays out. For any cryptographically signed ballot of the form D'(V), a voter will want to confirm one of three things:

This is my ballot.
This isn’t my ballot.
This isn’t anybody’s ballot.

The CEP allows legitimate voters to track their ballots. A voter N who has uploaded D'(V) and E’ onto the ledger of ballots will be able to find those two items digitally represented there and will be able to confirm that they match up to contribute a vote to Alice’s or Bob’s ledger of received votes. That’s great for voters confirming their own votes, but not for voters or concerned third parties attempting to disconfirm the votes of others.

Because the CEP treats votes as belonging to voters, votes created out of thin air (i.e., ascribed to voters who don’t actually exist, or phantom voters, as we’ll call them) or votes ascribed to actual voters who are not voting or otherwise paying attention could conceivably slip through the cracks. A vote created in the name of a live actual voter by registering this voter under a fraudulent proof of identity and setting up public-private key pairs unknown to the actual voter can be redressed once the voter challenges the bogus information entered in the voter’s name on the ledger of registered voters (recall the 5-tuple array; the actual voter will insist that it be changed).

Provided that the ballot, cryptographically signed by D’, has yet to be uploaded, a bogus array in the ledger of registered voters can be invalidated by the real voter, thus removing (E,D) and (E’,D’) from any authorization for uploading a ballot onto the ledger of ballots. This means, however, that the registration period for updating the ledger of registered voters needs to be separate from and precede the actual voting period during which cryptographically signed ballots and their keys are uploaded (unlike presently, where in some states voting and registration periods overlap).

This restriction should not pose a problem, however, since the CEP allows all voting to occur online and without delays, so all votes could be readily cast and confirmed on a single day. But if the registration period and the voting period are allowed to overlap, bogus ballots submitted during that overlapping time period in the name of real voters will be impossible to recall by the real voters. It’s like showing up at a polling place and being informed that the record shows you have already voted. At that point, it’s probably too late.

Finally, the creation, on the ledger of registered voters, of identities of voters that don’t even exist poses a distinct problem for the CEP. Basically, bad actors are in this case simply manufacturing voters and votes. While it will be possible to confirm that these phantom voters voted, it will not be possible, within the CEP, to recall their votes once the ballots in their names are cast or to know who they voted for.

The only recourse in the CEP for dealing with such phantom voters is to rule them out, as much as possible, from the ledger of registered voters from the start. Given that the registration period of voters will, within the CEP, strictly precede the voting period, it will be up to concerned third parties, and ideally the election commission itself, to make the PoI for voters sufficiently stringent so that only real voters can get past the gatekeeping safeguards and onto the ledger of registered voters.

The bottom line is that security against phantom voters must occur and can only occur by securing the ledger of registered voters. To the degree that fraud here abounds, it may be necessary to unmask PoI information about questionable voters and even insist on direct contact with and confirmation from them.

This problem of phantom voters, however, can be mitigated even if it cannot be totally eliminated. A crucial step toward mitigation, besides stringent PoI requirements, will be instituting a lag between the registration period for voters (during which their PoI data is entered on the ledger of registered voters) and the voting period (during which cryptographically signed ballots and corresponding keys are uploaded).

If the registration period ends at twelve midnight and voting begins right after, it could be that hundreds of thousands of new phantom voters are suddenly created out of thin air at 11:59pm (thereby placing them on the ledger of registered voters just before the deadline) and then vote at 12:01am (thereby upload their cryptographically signed ballots and keys just after the deadline). Enforcing a lag will provide a period during which phantom voters can be identified and weeded out (and the fraudsters responsible hopefully brought to justice).

5.11 Loose Ends and Loopholes

The CEP has many moving parts and those parts need to be suitably coordinated. To the degree they are, I’m persuaded the CEP can be made to work, guaranteeing free and fair elections. But the devil will be in the details. Take, for instance, the concern about phantom voters in the last subsection. Imagine a legitimate good-faith voter named N uploads at alice-v-bob-election.gov/ballots/ballot-upload a cryptographically signed ballot D'(V) by first providing and verifying ownership of the ballot via the private-public key pair (E,D) per the CEP. What is to prevent a corrupt election commission from substituting for D'(V) another ballot and then down the line uploading the key that unlocks it, thereby removing N’s legitimate ballot and putting another in its place?

As it is, because uploaded ballots will be visible online, N will instantly see that the rightful ballot D'(V) was not in fact uploaded. N will thus have cause for redress. If the election commission, in the ledger of registered voters, marks N as having voted, then N can forcefully probe what happened to D'(V) and why it is not appearing on the ledger of ballots. Because hash(D’) is next to N’s name in the ledger of registered voters, N can even reveal D’, proving both that this key belongs to N and that no cryptographically signed ballot using that key appears on the ledger of ballots. Making such a case will be a hassle for N, however, and with a sufficiently corrupt election commission, delays and smokescreens may skew the outcome of the election before N’s vote gets properly counted.

This problem has another variant. A thoroughly corrupt election commission could simply start uploading multiple ballots of the form D'(V) and then also upload the corresponding keys, causing votes to be counted but at the same time not even bothering to put check marks next to names in the ledger of registered voters to signify that a voter has voted. The election commission would thus bypass the upload procedure for cryptographically signed ballots. This would lead to a math inconsistency in that no registered voters would have their names marked off as having voted, but new cryptographically signed ballots would nonetheless be appearing. An arithmetic inequality would thus exist between the number of supposed votes checked off on the ledger of registered voters and the number of cryptographically signed ballots appearing on the ledger of ballots.

To avoid such an obvious math error, a corrupt election commission will be strongly tempted to manufacture phantom voters in the ledger of registered voters. Their names can then be checked off as having voted while uploading ballots cryptographically signed in their names. This puts a security burden on the ledger of registered voters, to make sure that no such phantom voters reside there. We addressed this point and ways to mitigate it in the last section, but the challenge will be to keep this problem firmly in check.

A particularly problematic point with secret ballots, and this is a problem for all elections that attempt to keep the identity of voters separate from their ballots, is the handoff of the ballot from voter to the election commission. At the moment of handoff, strange and spooky things can happen. In the digital context, there’s always the prospect of someone attaching a tracking pixel to the ballot. But even in a paper context, distinguishing marks can be added to make clear which voter cast which ballot. Such marks don’t even need to exactly identify a given voter. A paper ballot could have a seemingly stray mark if a voter is thought to belong to one party, another stray mark if a voter is thought to belong to another party. And perhaps ballots with the “wrong” stray mark will simply disappear.

I knew a professor who at the end of the term would hand out long student evaluations that required multiple sheets of paper. The professor would staple the sheets in different ways and give them accordingly to different students or groups of students. He could even use a unique staple location and orientation if he really wanted to know what one particular student was thinking about him. The point is that there are always ways to track information that is transmitted in a causal chain. Safeguards and penalties can help. Privacy statements on websites now carry liabilities if the websites don’t adhere to the terms of those statements.

Yet even without such shenanigans, there can be indirect ways to track voters and connect them to their ballots. Suppose voter N first proves his or her identity by means of the private-public key (E,D) and then uploads the cryptographically signed ballot D'(V). At the same time, the election commission marks N as having voted on the ledger of registered voters. Two events now are happening within a narrow window of time: N being shown to have voted on the ledger of registered voters and D'(V) appearing on the ledger of ballots. If few votes are cast at the time, temporal proximity may be enough to connect N with D'(V), thus undermining the secrecy of the ballot. It might therefore be best not to put a check mark next to a voter’s name right after he or she votes but to wait for a larger block of voters to have voted and then to mark all their names at the same time as having voted.

Like most cryptographic protocols, the CEP invites an arms race in which bad actors try to subvert it and good actors try to shore it up. Especially important will be decentralized safeguards. For instance, in addition to the use of data integrity methods, it will help to have independent third parties acting as poll monitors. A poll monitoring organization, for instance, could run a mirror site to alice-v-bob-election.gov so that whenever a voter N uses (E,D) to upload the cryptographically signed ballot D'(V), (E,D) is also used on the mirror site to upload D'(V). The same privacy restrictions would then have to apply to the poll monitoring organization as to the election commission so that it can’t publicly identify N, or any information that could be used to identify N, through the uploads.

The bottom line is that a successfully executed CEP will require careful consideration of what could go wrong as well as what needs to go right with it. A successful implementation of the CEP means understanding what bad actors might do to subvert it (thus committing election fraud), and what good actors need to do to keep it from being subverted (thus ensuring a free and fair election).

5.12 The Cryptosecure Election Protocol in a Nutshell

That’s the Cryptosecure Election Protocol. In a nutshell, it requires a server, such as alice-v-bob-election.gov, and then four ledgers or subdirectories (five if you count the ledger of eligible voters):

alice-v-bob-election.gov/alice
alice-v-bob-election.gov/bob
alice-v-bob-election.gov/registered-voters
alice-v-bob-election.gov/ballots
All four ledgers will be publicly viewable and tracked in real time with data integrity methods to ensure that no unwarranted changes are made. The ledger of registered voters comprises 5-tuples of the form (becoming 6-tuples when a vote is counted), with underlying proof of identity Z for N and two public-private key pairs (E,D) and (E’,D’), the private keys being known only to N.

When N writes up a ballot V that votes for either Alice or Bob, N uses E to authorize uploading D'(V), thus marking on the ledger of registered voters that N has cast a vote. And then, anonymously, N uploads E’. The uploads are then both visible at alice-v-bob-election.gov/ballots. Phantom voters can try to co-opt this approach to uploading ballots, so they must be stopped before it gets to that point by introducing strong protections against bogus proofs of identity and by introducing a lag between the time of voter registration and the time of actual voting.

Even though many locks and many keys will be uploaded onto the ledger of ballots, only one lock and one key can ever work together. When there is a fit, a vote is cast, mapped onto either Alice’s ledger or Bob’s. At each step, the voter knows exactly how the information and data he or she has inputted is being used and how it contributes or fails to contribute a vote to a candidate, all the while keeping the voter’s identity confidential.

Finally, even though the steps outlined here might seem daunting, in fact a single app could easily handle all the hash functions, QR barcodes, public-private key combinations, nonces, etc. described in the Cryptosecure Election Protocol, basically handling all the grunge work involved with proof of identity and uploading all crucial data.

Such apps, by simply following the protocol, can be multiply realized, with different companies providing the same functionality so that voters are not at the mercy of any one app development company. Most importantly, through the Cryptosecure Election Protocol, voters will be able to track their votes, see that they have been correctly counted, and be able to provide rock-ribbed evidence to the contrary if there is election fraud.

Note: A pdf of a slide presentation is available

You may also enjoy our earlier stories in this series:

How electoral fraud is different from financial fraud. Money can be moved around safely but votes must be credited to a single intended destination. Six suggestions are offered to reduce electoral fraud by enabling data integrity methods to be used throughout the process.

What if voters could sue for lost or altered ballots? Let’s look at the difference between what happens with financial fraud and electoral fraud. With financial fraud, the bank must make transactions good. With electoral fraud, the voter is, by contrast, just out of luck.

How do we know financial transactions are honest? Let’s look at the steps we can take to find out. Let’s ignore microthefts, in which fractions of pennies are skimmed off an account at every transaction—almost unnoticeable—what about the big stuff?

How can we prevent financial or election fraud? Both contexts come down to an accounting problem, keeping track of money or votes over time. Let’s take two people, the famous Alice and Bob, used to demonstrate many propositions in math and science and think of them as candidates running for office.

and

How can ballots be both secret and fair? The secrecy of ballots would not be compromised if voters usedsome markers of their identity known only to themselves. Fickser: If you cast a ballot, it is your ballot. If the ballot is cast by someone else in your name, you deserve to challenge it and get it changed.