Big Data Can Lie: Simpson’s Paradox
Simpson’s Paradox illustrates the importance of human interpretation of the results of data miningThere are many ways data analytics can lead to wrong conclusions. Sometimes a dishonest data cruncher interprets data to further her agenda. But misleading data can also come from curious flukes of statistics. Simpson’s Paradox1, 2 is one of these flukes.
Here’s an example. Baseball player Babe has a better batting average3 than Mickey in both April and May. So, in terms of batting average, Babe is a better baseball player than Mickey. Right?
No.
It turns out that Mickey’s combined batting average for April and May can be higher than Babe’s. In fact, Babe can have a better batting average than Mickey every month of the baseball season and Mickey may still be a better hitter. How? That’s Simpson’s Paradox.
Here are the data for the two consecutive months:
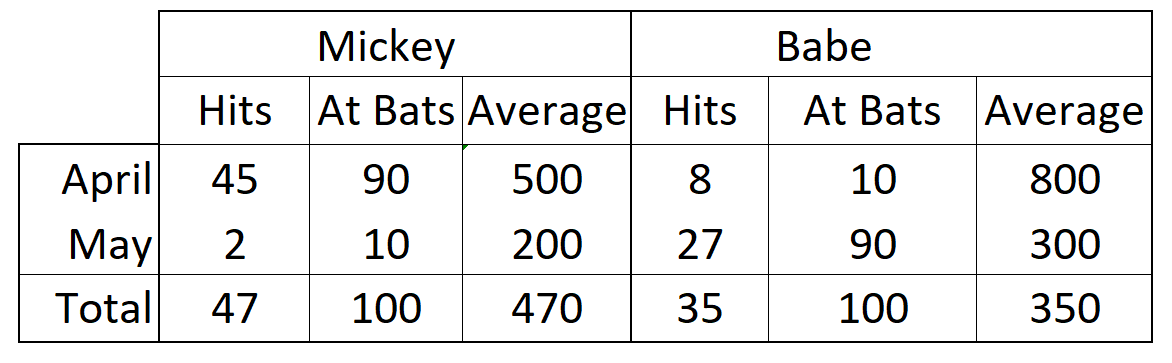
Simpson’s Paradox illustrates the importance of human interpretation of the results of data mining. Nobel Laureate Ronald Coase said, “If you torture the data long enough, it will confess.” Unsupervised Big Data can torture numbers inadvertently because aritifical intelligence is ignorant of the significance of the data.
What’s Going On?
Data viewed in the aggregate can suggest very different properties than the same data, examined in more detail, would. A more general view of Simpson’s Paradox is evident in the following animated gif 4 where experimental results of two variables are plotted.
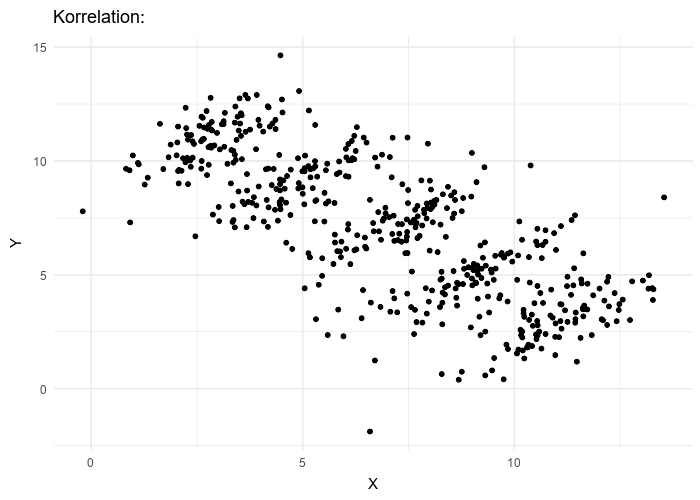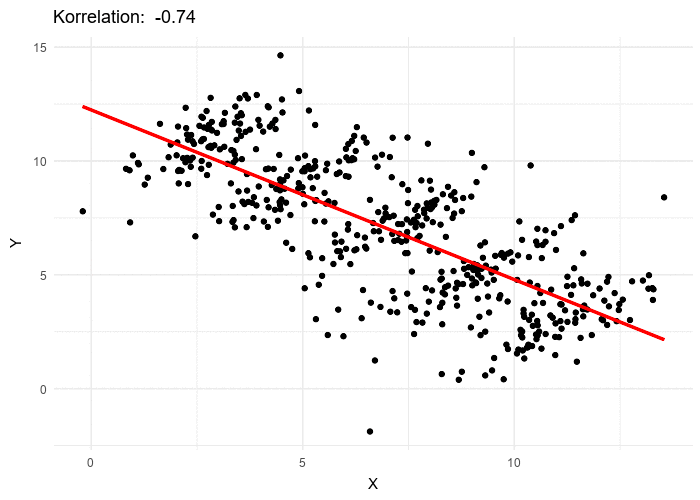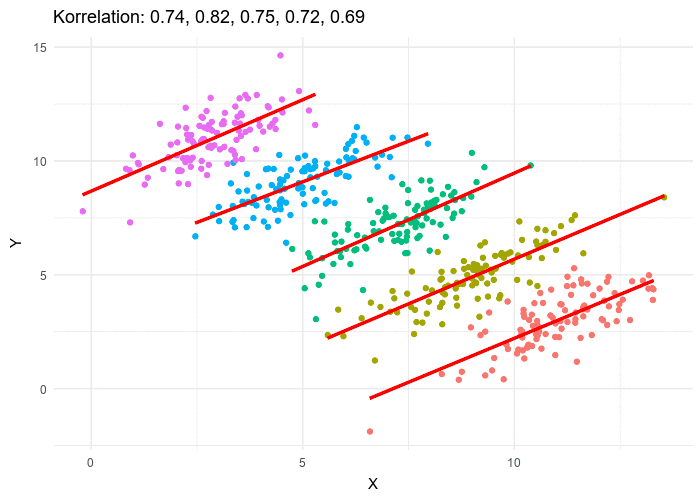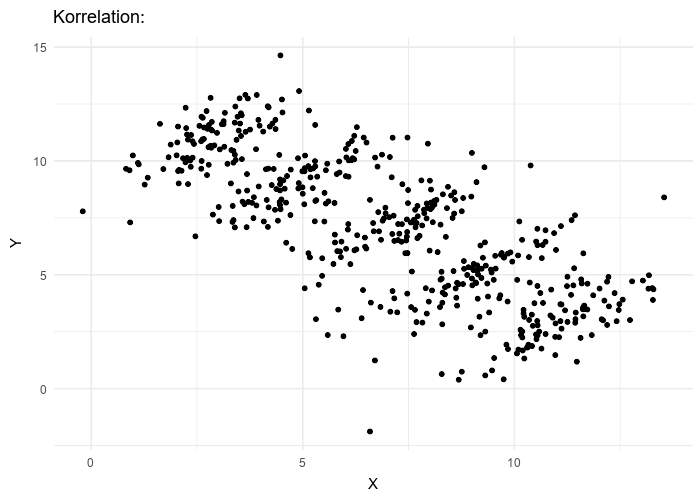
What is the overall trend if a line is fit to this data? If all the data is used, the trend line is decreasing. If five individual data clusters are identified and lines fit, we have, for each group of points, an increasing trend. The conclusions are opposites. Without knowing which points belong to which class, there is no right answer.
Clustering remains largely an art
An underlying cause of the challenge posed by Simpson’s Paradox is clustering, where individual data points in a big data set must be grouped into distinct groups (or clusters). Clustering is a heuristic, a practical method of problem-solving that remains largely an art. In the above figure, for example, do we keep all the data in one big cluster, divide it into two groups, or five groups, or ten? If we know nothing more about the data, there is no right answer. For this particular case, we might eyeball that there are five clusters of points in the figure. But in other cases, the points are more homogeneously distributed and it will not be as clear.
Even more challenging is characterizing data that represent 25 different variables instead of only two. Directly visualizing points in a 25-dimensional space is simply not possible for a human. A seasoned practitioner with domain expertise must spend some time becoming friends with the data before figuring which data point goes where. A human is needed to make things work.
Do we really need a human to identify the clusters? Backer and Jain 5 note
…in cluster analysis a group of objects is split up into a number of more or less homogeneous subgroups on the basis of an often subjectively chosen measure of similarity (i.e., chosen subjectively based on its ability to create “interesting” clusters)
Note the repeated use of the term “subjectively,” meaning a decision based on the judgment of a human. The criterion is that the clusters be “interesting.”
There is no universally agreed upon categorical definition of a cluster in mathematics.6 Which clustering procedure or clustering procedure class is used is a human decision.
Big Data Is Ignorant of Meaning
Simpson’s Paradox illustrates the need for seasoned human experts in the loop to examine and query the results from Big Data. Could AI be written to perform this operation? Those who say yes are appealing to an algorithm-of-the-gaps. They say it can’t be done now, but maybe they’ll develop computer code to do it someday. Don’t hold your breath.
1 Simpson, Edward H. “The interpretation of interaction in contingency tables.” Journal of the Royal Statistical Society: Series B (Methodological) 13, no. 2 (1951): 238-241. Blyth, Colin R. “On Simpson’s paradox and the sure-thing principle.” Journal of the American Statistical Association 67, no. 338 (1972): 364-366.
2 I first learned about the Simpson Paradox from reading a draft for a book titled The 9 Pitfalls of Data Science by Gary Smith and Jay Cordes (Oxford University Press, forthcoming) 2019. I highly recommend the book.
3 The batting average of a baseball player in percent is the number of a player’s hits divided be the number of times the player has batted.
4 Reproduced under the Creative Commons Attribution-Share Alike 4.0 International license. Wikipedia.
5 Quoted by Xu, Rui, and Donald C. Wunsch. “Survey of clustering algorithms.” (2005) from Backer, Eric, and Anil K. Jain. “A clustering performance measure based on fuzzy set decomposition.” IEEE Transactions on Pattern Analysis & Machine Intelligence 1 (1981): 66-75.
6 Xu, Rui, and Don Wunsch. Clustering. Vol. 10. John Wiley & Sons, 2008.
Also by Robert J. Marks: Things Exist That Are Unknowable: A tutorial on Chaitin’s number
See also: Too Big to Fail Safe? (cautions on overuse of Big Data in medicine)
