The solution to last Monday’s leaky bucket problem is, as Micro Softies go, fairly difficult. Before we dive into the solution, here’s this week’s simpler puzzle:

As Figure 1 shows, there are three bags, each containing 100 marbles. One bag contains only black marbles, one only white marbles, and the other a mixture of black and white marbles. All three bags are labeled incorrectly. Here’s the question. How many marbles do you have to take from which bags in order to label all the bags correctly?

The answer is simple but fascinating.

Solution to Micro Softy 16: The Leaky Bucket        

Figure 2 below shows the cylindrical leaky bucket that was the topic of last week’s Micro Softy. Where should a hole be punched in the hollow cylinder wall so that the water goes as far from the cylinder as possible? A hole punched at the bottom will come out fast but has no room to fall. Its squirt distance is zero. A hole punched at the very top will come out with a velocity of zero, so will trickle down the side of the cylinder. Its squirt distance is also zero. So the maximum squirt distance must be from a hole somewhere between the top and the bottom.

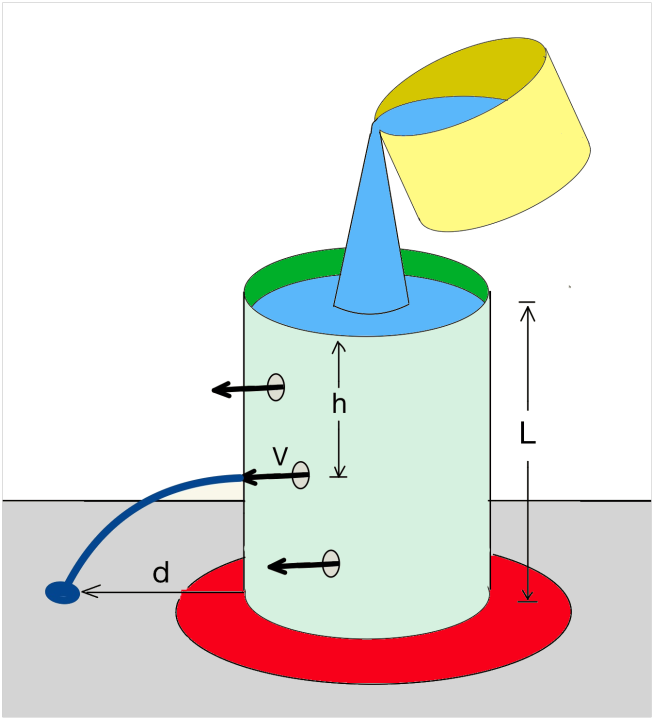
Where exactly the hole should be punched is not obvious but if you guessed it should be somewhere halfway down, you’d be right.  

 For my fellow nerds, here’s the math:

Torricelli’s law from fluid dynamics says that the velocity of the water squirt is v=sqrt(2gh) where g is the acceleration due to gravity. (This comes from equating the kinetic energy ½ mv² with the potential energy mgh and solving for v.)  Newton says an object dropped from a height of L-h takes t seconds to hit the ground where t=sqrt(2(L-h)/g). The distance the water squirts is therefore d=vt=sqrt(2h(L-h)).  This distance is maximum at a height of h=L/2 or at the halfway point of the cylinder. (To show this, take the first derivative of d and set to zero.)

And on the Moon?

The second part of the question asks, what difference does it make if we are on the Moon? Interestingly, when h=L/2, the maximum distance, dmax= L/sqrt(2) = 0.707 L (70.7% of the cylinder’s height), is independent of the acceleration due to gravity,  g. So, curiously, this maximum squirt distance is the same whether you are on the Earth or on the Moon.

Here are the puzzles (and solutions) from the last five Mondays:

Monday Micro Softy 12: Can You Connect the Dots? You may use no more than four perfectly straight lines and the lines must be connected. This classic puzzle in simple graph theory resulted in a commonly used phrase. Can you guess it?

Monday Micro Softy 13: Garbage Trucks, String Theory… … and Stained-Glass Windows. What connects them? These puzzles, associated with the great mathematician Leonard Euler (1707‒1783), have a practical use, for example, in laying water pipes.

Monday Micro Softy 14: How Did the Blind Ticket Seller Know? This puzzle doesn’t require math skills so much as advanced common sense reasoning. About last week’s solution, given here: If you code, the second part of the puzzle could also be offered to a computer.

Monday Micro Softy 15: What Happens to the Hole in a Hot Washer? When a washer ring is heated, does the hole in the center get bigger or smaller? The answer to last week’s Micro Softy turns on the question of what form of currency Claire gave the blind ticket seller. Did you guess it right?

Monday Microsofty 16: The Leaky Bucket. The puzzler must decide where to place the hole for maximum distance of outward flow. And explain how the problem would change on the Moon. One hint for the solution to the hot washer problem, given here, is the old trick for getting a tight lid off a jar: Running hot water over it.

Note: At Monday Micro Softy 11: What Happened to That Other Dollar?, you will also find links to the first ten Micro Softies. Have fun!