Vector algebra is the manipulation of directional quantities. Vector algebra is extremely important in physics because so many of the quantities involved are directional. If two cars hit each other at an angle, the resulting direction of the cars is based not only on the speed they were traveling, but also on the specific angle they were moving at.

Even if you’ve never formally taken a course in vector algebra, you probably have some experience with the easiest form of vector algebra — complex numbers (i.e., numbers that include the imaginary number i). In a complex number, you no longer have a number line, but, instead, you have a number plane. The image below shows the relationship between the real numbers and the complex numbers:

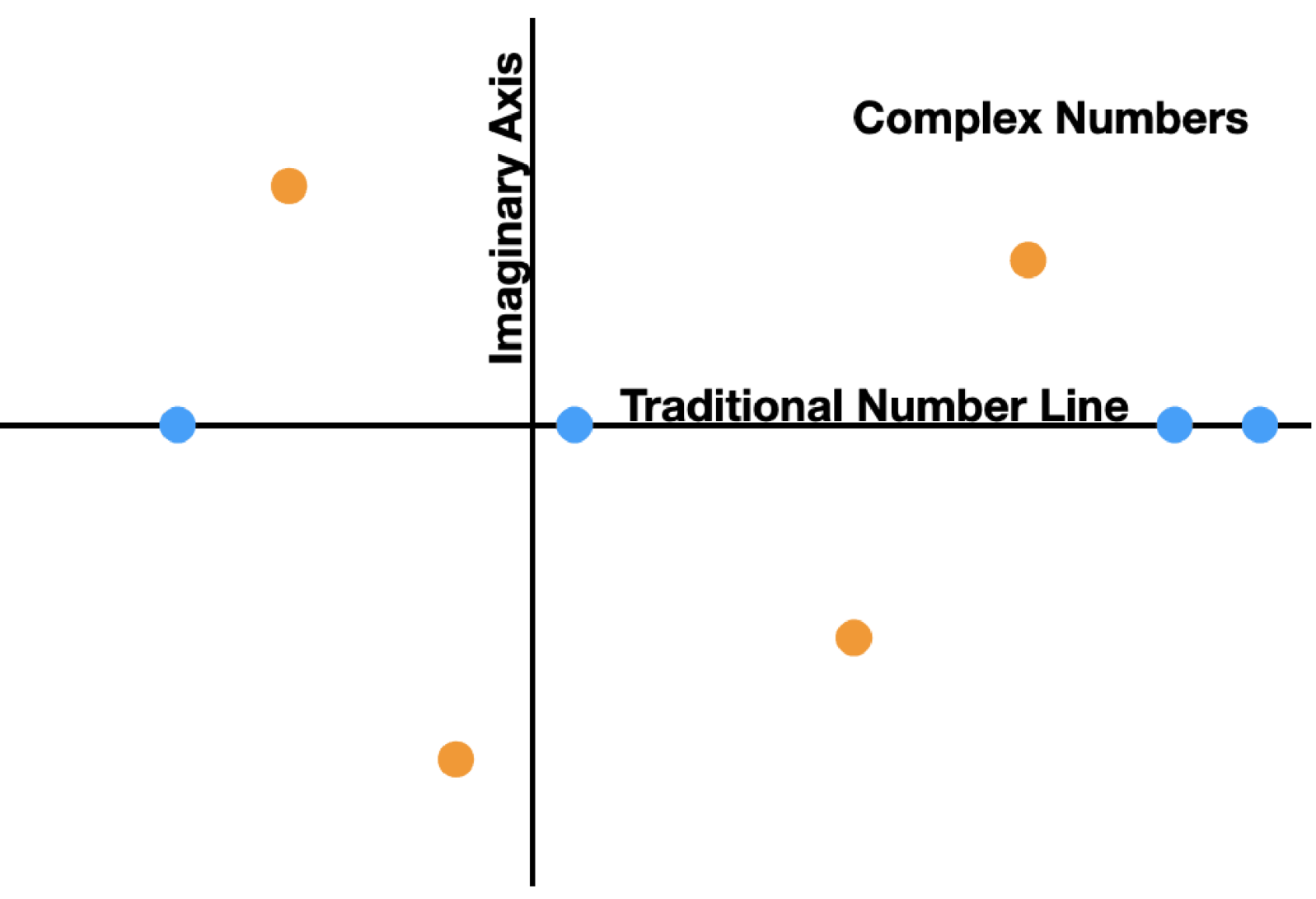
As you can see, the traditional number line is embedded in the complex plane. That means that, a traditional real number is just a complex number without any imaginary part. Complex numbers are usually written as A + Bi, where A is the distance along the traditional number line, and B is the distance along the imaginary axis.

Complex numbers can represent vectors by simply treating the points as actually being a vector out from the origin to the represented number. Below, we can see how the numbers in the above graph are thought of as vectors:

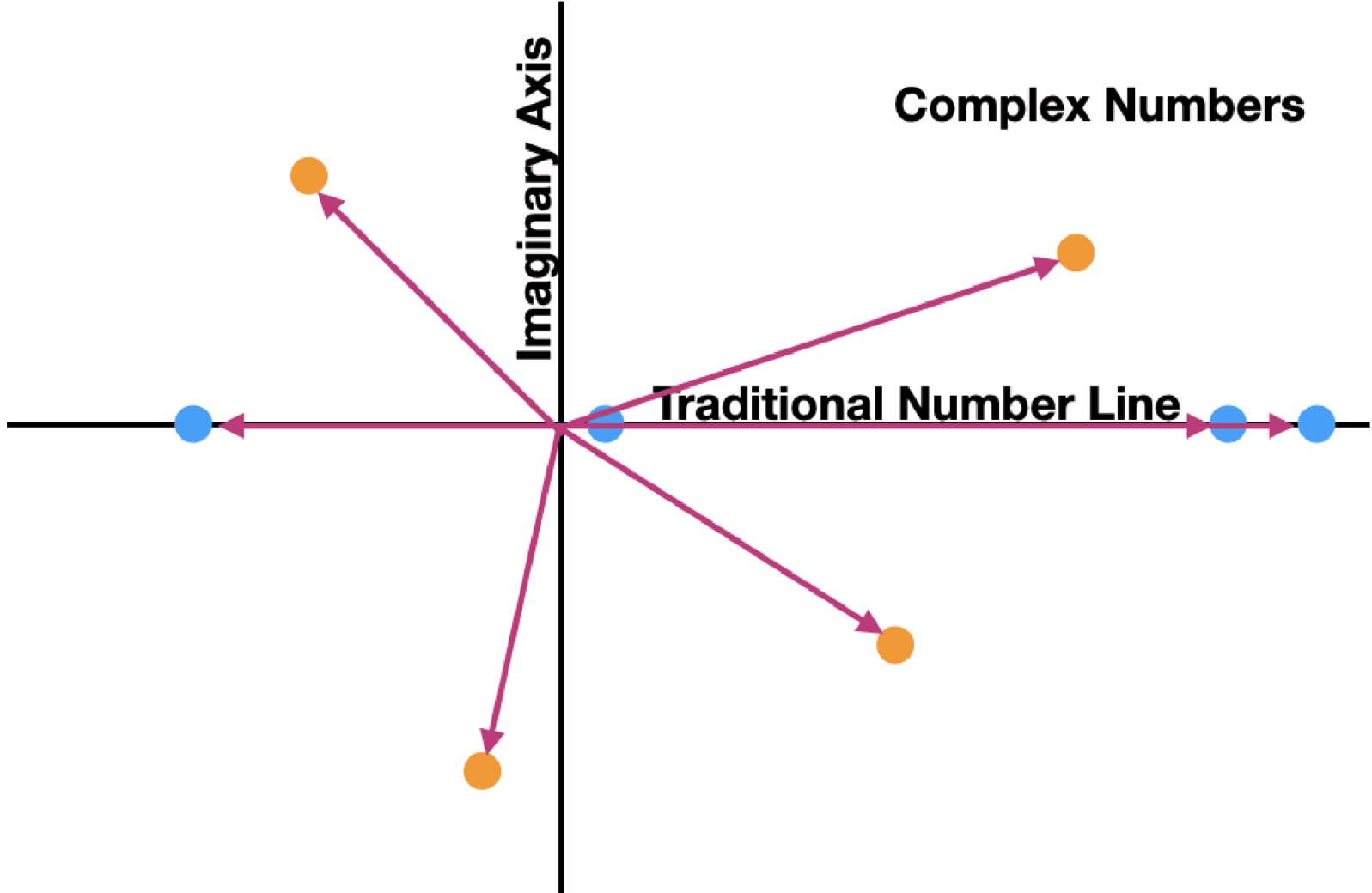
Positive numbers on the traditional number line represent vectors with an angle of zero degrees and negative numbers represent vectors with an angle of 180 degrees. Using this as a baseline, you can eyeball that the upper-right complex number here is at about 20 degrees. Therefore, using complex numbers, we can represent both a size (the length of the vector) and a direction (the angle at which the vector is oriented).

Imaginary numbers make representing and manipulating vector quantities extremely simple. Most students learn to add, subtract, multiply, and divide using complex numbers in high school.

This sounds great, so what’s the fuss?

It turns out that there is a well-recognized, deep problem with using complex numbers as vectors; they only really work with two dimensions. After that, the mathematics no longer works.
This has prompted all sorts of attempts to rectify the situation for 3-dimensional and higher dimensional vectors, in what is sometimes referred to as the “vector algebra war.” Some methods for representing higher dimensions include:

● Quaternions These were developed in 1843 by William Rowan Hamilton (1805–1865) as a way of expanding imaginary numbers into three dimensions.

However, it only works for three dimensions — and squaring a quaternion results in a sign that is opposite what it should be. This meant that they were generally good for managing rotations, but failed in other important ways.

● Complex spinors These were developed to describe quantum mechanics. However, it turned out that they were actually isomorphic to quaternions (i.e., they represented the same things and had the same benefits and deficiencies).

● Gibbs vectors In this representation, a vector is simply represented by a three-dimensional point (much like the complex numbers). However, this led to a lot of mathematical limitations and extra manipulations. It separated out multiplication into the “cross product” and the “dot product,” but did not have an equivalent division operation.

● Other vector systems have been used as well, each with its own difficulties.

In short, while complex numbers provide a straightforward way of representing vectors in two dimensions, there has been much historical disagreement on how to extend this use to more dimensions. Most of the answers have severe limitations.

How did Clifford algebra help resolve the problem?

The mathematician William Kingdon Clifford (1845–1879) developed a generalization of all of these in 1878, using a formalism that is known as either “Clifford Algebra” or “Geometric Algebra.” Clifford noticed that the existing approaches to vector algebra were either focused on static values (e.g., Gibbs vectors) or operational/relationship values (e.g., quaternions). Clifford combined these approaches into a unified relationship, which we know today as Clifford algebra.

The details of Clifford algebra are too complicated to go in to for our purposes just now. Its ability to not only fix the problems of generalizing vectors but also to simplify the resulting physics equations is extremely impressive. Clifford algebra involves some complicated operations; however, once you assume its mechanics, everything else becomes a trivial instance of it.

One of the better-known examples of this effect is Maxwell’s equations for electromagnetism. Maxwell defined four separate equations for understanding electromagnetic behavior. Don’t worry if you don’t understand what these equations mean. What we are really examining here is their complexity:

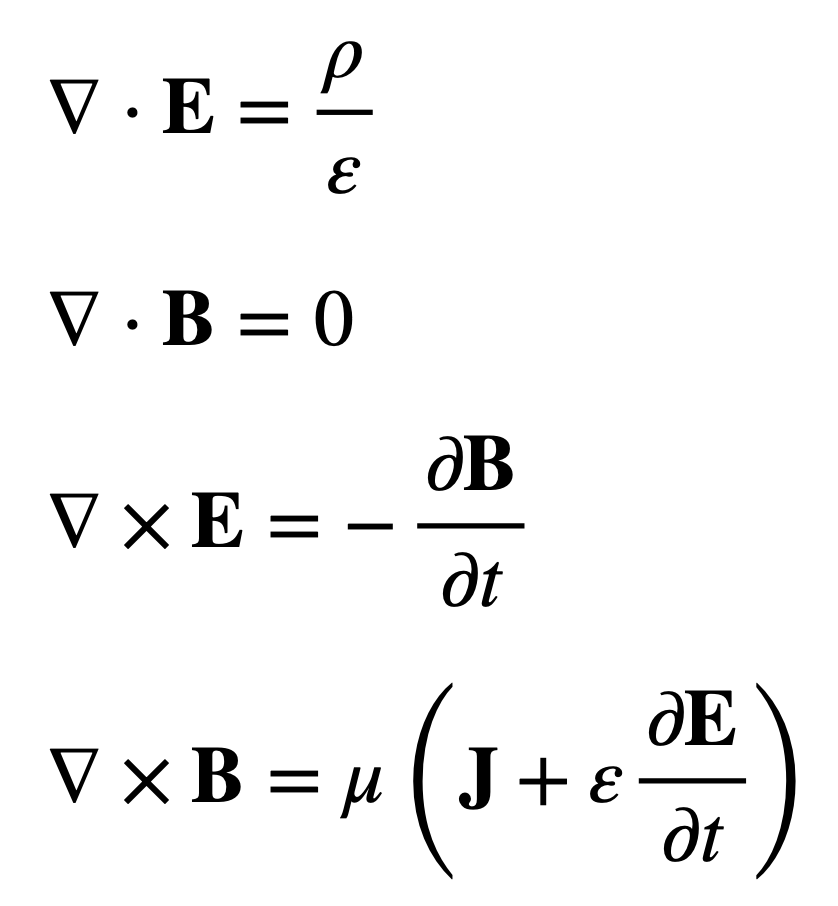
However, it turns out that all four of these can be unified using Clifford algebra. As noted by Chappell et al., using Clifford algebra, these four equations can be understood simply as:

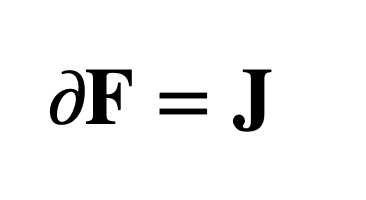
This is interpreted as the gradient of the field F (which is a combination of the electric and magnetic fields) is equal to the sources present J (which, here, is a combination of charges and currents in this formula).

In short, what once appeared as a really strange phenomena of electricity (needing four complicated equations to adequately describe) becomes a rather straightforward statement once the right formalism for understanding vectors is established.

Despite the fact that Clifford algebra is almost 150 years old, it has still not garnered the mainstream appreciation that it deserves, despite simplifying many equations and bypassing many kludges.

You may also wish to read: The needless complexity of modern calculus. How 18th century mathematicians complicated calculus to avoid the criticisms of a bishop. The fact is, calculus is taught in such a convoluted way that the natural beauty of it is almost always greatly distorted. (Jonathan Bartlett)